This is a partial answer.
I would say the hardest part is likely finding the points of intersection. In this post I discuss the generic approach, which involves solving a quadratic equation of at least degree $3$. However, since your ellipses are both centered around the origin, a quadratic equation will suffice.
Rewrite your ellipses in the following form (by expanding the numerator of the form you say you have):
$$a_1x^2+b_1y^2+c_1xy=d_1\qquad a_2x^2+b_2y^2+c_2cy=d_2$$
Then you can combine them: take $d_2$ times the first equation minus $d_1$ times the second and you get
$$(a_1d_2-a_2d_1)x^2+(b_1d_2-b_2d_1)y^2+(c_1d_2-c_2d_1)xy=0$$
This is the equation of a pair of lines passing through the origin and through the points of intersection. Next compute
$$t = \sqrt{(c_1d_2-c_2d_1)^2-4(a_1d_2-a_2d_1)(b_1d_2-b_2d_1)}$$
The lines are now described by one of these equations:
\begin{align*}
2(a_1d_2-a_2d_1)x + (c_1d_2-c_2d_1\pm t)y &= 0 \\
(c_1d_2-c_2d_1\pm t)x + 2(b_1d_2-b_2d_1)y &= 0
\end{align*}
Generally just picking one of these two equations is enough, since with the $\pm$ in it it will already give you both the lines. If you are unlucky, though, and one of the lines coincides with one of the coordinate axes, then either $(a_1d_2-a_2d_1)$ or $(b_1d_2-b_2d_1)$ will be zero. Using the equation with the zero there will cause one of the equations to become $0x+0y=0$ for one of the cases of the $\pm$. In those cases better use the equation where there is no zero.
Now you have the equation of a line, and you can intersect that with the ellipse. And then you have the points of intersection, and can use these for angle computation. I will not include all details for that in my answer, but I invite other answers to cover these parts.
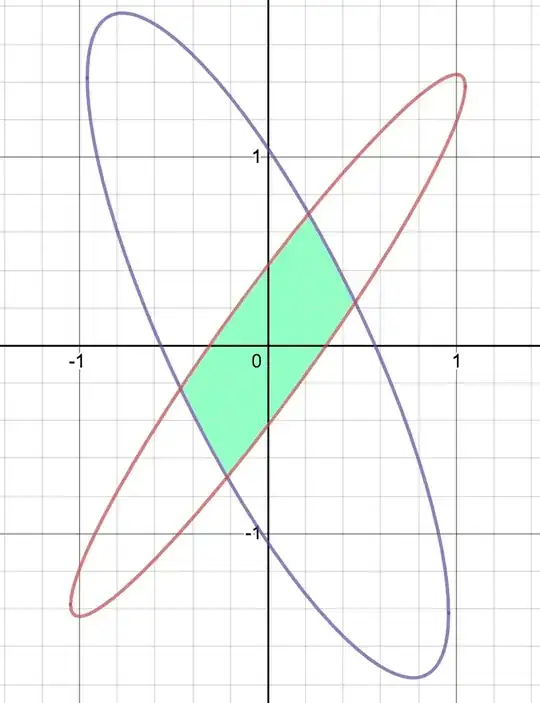
h, andkare zero. – Sia Rezaei Aug 03 '19 at 21:37$$\begin{array}{rcl} ax^2+bxy+cy^2<1 & \cap & cx^2-bxy+ay^2<1 \ A &=& \dfrac{8}{\sqrt{4ac-b^2}} \tan^{-1} \sqrt{\dfrac{a+c-\sqrt{(a-c)^2+b^2}}{a+c+\sqrt{(a-c)^2+b^2}}} \ a+c & > & 0 \end{array}$$
– Ng Chung Tak Aug 04 '19 at 10:10