18

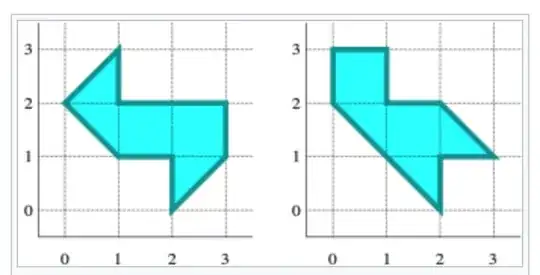
I want to make an algorithm grouping all the details having the same shape. each detail is defined by its surface, and a list of contour lines.

First I believed that having the same perimeter length and same surface would be enough, but I saw on that link that it is wrong hypothesis.

If I take as additional condition that the two shapes have the same number of segments, would it be enough? Or else how can I check that?

The problem is for each detail, they can get rotation, or symmetry.

Edit :

Thanks for your answers, I finally found a way to solve the problem (answer below)

Siegfried.V
  • 336
  • Wouldn't a kite/parallagram be a counter example? I think it'd be very hard to find the precise conditions that will allow you to say definitively: you can't cut a shape up into pieces are rearrange them with the same perimeter. Number of legs is certainly not enough. – fleablood Jul 25 '19 at 06:06
  • @stevengregory yes, but the linked answer was regarding 2 details with same surface and perimeter. I am trying to find a solution taking more parameters in account, as number of segments, or list of angles between segments... I think if I take in account list of segments with the list of their length and list of angles between each segment that would be enough. – Siegfried.V Jul 25 '19 at 08:06
  • Well I found solution, will first test it when working, then post my answer here, thanks anyway. – Siegfried.V Jul 25 '19 at 12:34
  • Can't look for it now, but there was an interesting video on the Numberphile youtube channel this month talking about how to detect uniqueness of a shape (or a similar issue, I'm not sure). You might want to see it. – Mark Jul 25 '19 at 15:39
  • @Mark found solution, I am now developping it, I write answer later when I finish to test it. Just excuse me I am new on "Mathematics" stack (I use to be on stackoverflow), may my answer e graphical, or can I explain it with a bit of code? – Siegfried.V Jul 25 '19 at 15:56
  • @Siegfried.V I'm even newer here than you, so don't ask me :D Also I'm not really interested in your problem per se, I was just browsing and thought that I might share what little I can. – Mark Jul 25 '19 at 16:01
  • One way of being sure two shapes are the same is to compare the distances between all the segment endpoints (not just the adjacent endpoints). If you can pair off the endpoints of each of the shapes so the distances are the same for each, then the two shapes are congruent. – Paul Sinclair Jul 25 '19 at 17:01
  • @PaulSinclair wow very good, seams easier than my solution... if you could add your own answer so I accept it, this would be good. Anyway to check if there is a symetry or not it is not enough(if you have some suggestion would be welcome), same to check each radius(my fault, I didn't precise there are also arcs). – Siegfried.V Jul 25 '19 at 17:06
  • @PaulSinclair in fact I just understood it is not working in my case (or didn't understand the answer?), because I don't know where is the starting point for each shape. So anyway I would need to calculate every distances from each point to each other point(for rectangle need to calculate 34 = 12 distances, right? for hexagone 56=30 distances. – Siegfried.V Jul 25 '19 at 17:16
  • Possibly the generalized hough transformation contains some way of representing a shape in a suitable way... At least it's used to find occurances of shapes provided as input in an image... – fabian Jul 25 '19 at 18:13
  • Possibly of interest: https://math.stackexchange.com/q/877424/18398 – JRN Jul 26 '19 at 00:30
  • @Joel no. In fact this is the same link as the one I shared, and if U look I added condition "number of segments" that is not enough as well demonstrated by Eevee. Anyway I found the solution in my post below, it is working perfectly. – Siegfried.V Jul 26 '19 at 04:03
  • @Siegfried.V "this is the same link as the one I shared" No. The one you shared has the title "Can two figures […]". The one I shared has the title "Polygons with equal […]". – JRN Jul 26 '19 at 04:48
  • Are any pair of chiral shapes not enough of a counter-example, since they are not superimposable? Or are they still the same "shape"? – Tom Jul 26 '19 at 08:43
  • JoelReyesNoche ahah nice, didn't notice :). @Tom in fact counter example from Hagen von Eitzen was very clear, but I expected to also find a solution on how to solve that(forgot I was on mathematical forum so people just answer "logically"). Will accept his answer as it answers to initial question perfectly, just for next people interested, I leave my solution to solve the problem. – Siegfried.V Jul 26 '19 at 10:07
  • @Siegfried.V You may also be interested in "Can you hear the shape of a drum?" where a much large collection of invariants is investigated and found to be insuffcient – Hagen von Eitzen Jul 26 '19 at 13:08
  • @HagenvonEitzen excuse me but I don't see the point, I first believed it was a joke (never heard about it), then read about it(wikipedia), but what I read is some different shapes can sound the same, so I don't see how this could help? – Siegfried.V Jul 26 '19 at 13:54

7 Answers7

85

In the spirit of the no-words answer to the linked question:

two shapes made up of squares which have the same perimeter and area but which are different shapes

Andrew Stacey
  • 3,273
Hagen von Eitzen
  • 374,180
  • 10
    I like the simplicity of this, because the demonstration of a single counterexample is sufficient to disprove the conjecture. That ends the discussion nicely. – Monty Harder Jul 25 '19 at 16:14
34

Inspired by Hagen von Eitzen's answer, a particular pair of tetrominoes furnishes another counterexample (minimal among polyominoes):

enter image description here

Travis Willse
  • 99,363
14

No, it is still not enough. Even for quadrilaterals it is not enough. Take a kite with sides $1,1,3,3$ and the angle between the two $1$s a right angle. The perimeter is $8$ and the area is $\frac 12(1+\sqrt{17})$. Now take a rhombus with sides of $2$. It also has a perimeter of $8$ and you can choose the angle to make the areas match. It is even worse for more sides. The area and perimeter are just two constraints, while there are lots of degrees of freedom.

Henry
  • 157,058
Ross Millikan
  • 374,822
  • ok thanks, can you see my edit please? – Siegfried.V Jul 25 '19 at 06:37
  • found a solution, will first test in in practical, then post it here – Siegfried.V Jul 25 '19 at 12:35
  • 2
    Here is a more complex example that refutes a weaker version of the asker's idea. Even if you specify that it is a quadrilateral, and you specify that the side lengths taken in order are $1, 1, 3, 3$ (which is stronger than merely requiring the perimeter to be $8$, of course), and specify that the area is $\frac12 (1+\sqrt{17})$, that still does not determine the quadrilateral up to congruence (no angles are specified). The reason is that it can be either the convex kite you mentioned, or a non-convex "arrowhead". – Jeppe Stig Nielsen Jul 26 '19 at 22:38
  • 1
    (continued) For some areas, like $2.9$ (any number between $2\sqrt 2$ and $3$ should work), the two non-congruent quadrilaterals with sides taken in order $1,1,3,3$ are both convex. – Jeppe Stig Nielsen Jul 26 '19 at 23:04
8

enter image description here

Possibly the simplest counterexample: Form two sides of a triangle with line segments of unequal length. In one version, mirror it. In the other, rotate it 180°.

Gnubie
  • 445
3

Well, I finally managed to do that, but it was longer than expected :

My shape is defined by a list of Contour element, Contour is defined by 2 points and a radius.If this is a segment then radius=0, if this is an arc, radius is positive if I turn in trigonometric direction, negative if opposite side).

I make a first check, checking if areas are equal(just to identify faster if shapes are equal or not).

For each shape, I browse each segment(or circle arc) ClockWise direction and I return 3 results :

  • List of the lengths of segments(just Pythagoras, don't check radiuses)
  • List of radiuses of each segment/arc
  • List of angles between each segment and consecutive segment

I then can compare them (let's take in account that I start from the same point on each figure). In C# I just made a loop trying to start from different points.

If all 3 lists are equals, this means the shapes are equal and without rotation.

Then for symmetry problem I just will recalculate 3 above lists for second shape, but browsing contours in opposite direction, if the results are equal(angles and radiuses just will be opposite sign), so it is the same shape with symmetry.

Siegfried.V
  • 336
  • 5
    It is good that you have solved your problem, but this does not answer the question that you asked. – Rory Daulton Jul 26 '19 at 15:26
  • 2
    @RoryDaulton exactly, in fact I didn't formulate correctly question, that's why I accepted the other answer that answered perfectly, just added that answer for who would meet the same problem. – Siegfried.V Jul 26 '19 at 15:47
  • 1
    @RoryDaulton - Actually, it does directly answer the question asked in the OP itself. It is only the question in the title that is not answered by it (and therefore appropriate that Siegfried V has accepted Hagen von Eitzen's answer to that question). – Paul Sinclair Jul 26 '19 at 16:46
  • 1
    Depending on how many times you have to check for equality, it might make sense to enforce a canonical starting vertex, rather than looping over all possible starting vertices. For instance: define a sorting function on the triples (length, radius, angle), and when you create your objects make sure that each list of triples is the smallest (lexicographically) among its cyclic permutations. If you implement it properly, I think it should cost O(n log n) to create a shape with n edges, and O(n) to compare them, rather than O(n) to create them and O(n^2) to compare them. – Federico Poloni Jul 28 '19 at 09:45
  • @FedericoPoloni In fact that's a good idea, not only for time spent, but the code would be easier to implement. But not totally sure this would work if I don't take segments in the good order (symmetry)? How do you imagine that sorting function? In my case I think this wouldn't work (not sure), because I also have to check if each segment has some chamfers (can call it 3D?) and each detail has some drillings inside so for Drilling I calculate a List of distances between each drill and each of the angles of my shape. Thanks anyway for the idea that I will look at, just for simplifying my code. – Siegfried.V Jul 28 '19 at 11:10
0

A famous problem was posed in 1966, "Can you hear the shape of a drum?" That is, can you find two different planar domains whose spectrum is the same? It was known that any two such domains must have the same area and the same perimeter. The question was answered negatively by Gordon, Webb and Wolpert in the early 1990s. Here is their example:

enter image description here

Notice that the number of sides is also the same, so this answer's the OP's question with even more conditions imposed.

Marc Chamberland
  • 109
-1

Yes, as others have demonstrated, you can have different shapes given the same area, perimeter, and number of segments.

Furthermore, it seems to me you can have different shapes given any number of arbitrary metrics. Take this terrible looking key, for instance:

enter image description here

You could easily imagine an infinite number of keys like this each uniquely represented by 7 numbers. For this key, those values would be 2, 3, 1, 2, 3, 1, 2.

These need not be integers.

You could imagine a million-toothed key being uniquely represented with a million numbers.

Now, technically you can use a single real number to represent a million real numbers. However, I don't believe any such function that does this conversion is continuous, and so likely isn't useful for you. When they aren't continuous, you'll have metrics like 5.213283 and 5.213284 represent wildly different shapes.

I would consider perimeter and area nice, continuous metrics. Any small perturbations to the points of the polygon result in a small change in those values.

Note: I could be completely wrong. I look forward to looking up that numberphile video later today.

Community
  • 1
Geoffrey
  • 99
  • Well that's nice, but nothing new regarding other answers, the question was more, how to solve that, even if I didn't formulate it correctly in title. Anyway I found how to do it(answer below). – Siegfried.V Aug 09 '19 at 02:45