The complement of a trefoil has so-called $\widetilde{\mathrm{SL}_2(\mathbb{R})}$ geometry, according to Thurston's classification, since one can show that $\mathrm{SL}_2(\mathbb{R})/\mathrm{SL}_2(\mathbb{Z})$ is diffeomorphic to a trefoil complement. The preimage of $\mathrm{SL}_2(\mathbb{Z})$ in the universal cover $\widetilde{\mathrm{SL}_2(\mathbb{R})}$ is known as $\widetilde{\mathrm{SL}_2(\mathbb{Z})}$, and the geometry of the trefoil complement comes from the quotient space $\widetilde{\mathrm{SL}_2(\mathbb{R})}/\widetilde{\mathrm{SL}_2(\mathbb{Z})}$. Since both groups contain the normal subgroup $\{\pm I\}$, these quotients are the same as the quotient space $\mathrm{PSL}_2(\mathbb{R})/\mathrm{PSL}_2(\mathbb{Z})$. It should also be pointed out that since $\widetilde{\mathrm{SL}_2(\mathbb{R})}$ is simply connected and $\widetilde{\mathrm{S}_2(\mathbb{Z})}$ has no torsion, the fundametal group of a trefoil complement is $\widetilde{\mathrm{SL}_2(\mathbb{Z})}$, which is also known as the three-strand braid group.
Trefoil knots, being torus knots, are Seifert fibered spaces, which are not hyperbolic---however, $\mathrm{SL}_2(\mathbb{R})$ fibers over $\mathbb{H}^2$ by having it act on the upper half plane by Möbius transformations, so it is sort of (but not quite) $\mathbb{H}^2\times \mathbb{R}$ geometry. For an orientable irreducible $3$-manifold with an infinite fundamental group (like the trefoil complement), it is the case that it has a nontrivial cyclic normal subgroup if and only if it is a Seifert fibered space. The way such a cyclic normal subgroup arises is as the kernel of a map $\pi_1(M)\twoheadrightarrow\pi_1^{\mathrm{orb}}(B)$, where $M$ is the Seifered fibered space, $B$ is the "base orbifold" from collapsing each fiber to a point, and $\pi_1^{\mathrm{orb}}$ denotes the orbifold fundamental group. Recall that $\pi_1(M)$ acts on its universal cover $\widetilde{M}$ by deck transformations. If $M$ is Seifert fibered, then $\widetilde{M}$ has an induced fibration by lines and circles, and the deck transformations carry fibers to fibers, and thus $\pi_1(M)$ acts on the base orbifold $\widetilde{B}$, which is the quotient of $\widetilde{M}$ by collapsing fibers to points. The group $\pi_1^{\mathrm{orb}}(B)$ acts on $\widetilde{B}$ by the orbifold equivalent of deck transformations, so we have a homomorphism $\pi_1(M)\to \pi_1^{\mathrm{orb}}(B)$. It turns out that this map is surjective with an infinite cyclic kernel generated by any non-expectional fiber of $M$.
A special kind of normal subgroup is the center, and in fact every knot complement whose fundamental group has a nontrivial center is a torus knot. More generally, in the case of the kernel of the above map being infinite cyclic, it is central if and only if $B$ is orientable. (Torus knots are the only knots with a Seifert fibered complement, and each has an orientable base orbifold.)
In the case of $M$ being the trefoil complement with the standard Seifert fibration with two exceptional fibers, $B$ is an orbifold that is a disk with two singular points of orders $2$ and $3$, which is known as a "$(2,3,\infty)$ turnover." This is exactly the orbifold quotient $\mathbb{H}^2/\mathrm{PSL}_2(\mathbb{Z})$ (whose fundamental domain in $\mathbb{H}^2$ is pictured on the cover of The Topology of Numbers; the orbifold points come from the order-$2$ symmetry about edges and the order-$3$ symmetry about centers of triangles). Since $\mathbb{H}^2$ is simply connected, $\pi_1^{\mathrm{orb}}(B)\cong \mathrm{PSL}_2(\mathbb{Z})$, hence the map $\pi_1(M)\twoheadrightarrow\pi_1^{\mathrm{orb}}(B)$ is $\widetilde{\mathrm{SL}_2(\mathbb{Z})} \twoheadrightarrow \mathrm{PSL}_2(\mathbb{Z})$. To remind ourselves what this map does, consider the commutative diagram of short exact sequences
$\require{AMScd}$
\begin{CD}
0 @>>> \mathbb{Z} @>>>\widetilde{\mathrm{SL}_2(\mathbb{Z})} @>>> \mathrm{PSL}_2(\mathbb{Z}) @>>> 0\\
@. @| @VVV @VVV @. \\
0 @>>> \mathbb{Z} @>>>\widetilde{\mathrm{SL}_2(\mathbb{R})} @>>> \mathrm{PSL}_2(\mathbb{R}) @>>> 0
\end{CD}
The bottom row is the universal cover of $\mathrm{PSL}_2(\mathbb{R})$, whose kernel is $\mathbb{Z}$ since $\pi_1(\mathrm{PSL}_2(\mathbb{R}))=\mathbb{Z}$. All the vertical maps are inclusions, and the top sequence is short exact by construction (it is a pullback). The $\mathbb{Z}$ in the upper left is the center of $\widetilde{\mathrm{SL}_2(\mathbb{Z})}$ essentially by the argument you give in your question (also seen in Hatcher's Algebraic Topology, Example 1.24), but you can also say something about pullbacks and classifying central extensions.
One thing you can take from this is that the space $\widetilde{\mathrm{SL}_2(\mathbb{R})}$ is a natural space in which to embed a Cayley graph for $\widetilde{\mathrm{SL}_2(\mathbb{Z})}$. The group $\widetilde{\mathrm{SL}_2(\mathbb{Z})}$, being a subgroup, acts on $\widetilde{\mathrm{SL}_2(\mathbb{R})}$ by multiplication, so it also acts on the embedding of the Cayley graph. (Hatcher's Algebraic Topology, Example 1.35 gives an explanation of the Cayley graph itself.) The $\mathbb{Z}$ "axis" of $\widetilde{\mathrm{SL}_2(\mathbb{R})}$ spans a geodesic line $L$, and the image of $L$ in $\mathrm{PSL}_2(\mathbb{R})$ is $\mathrm{PSO}_2(\mathbb{R})$. Thus, collapsing the universal cover in the $L$ direction (that is, taking the space $\{gL:g\in \widetilde{\mathrm{SL}_2(\mathbb{R})}\}$) gives the space $\mathrm{PSL}_2(\mathbb{R})/\mathrm{PSO}_2(\mathbb{R})$, which is $\mathbb{H}^2$. Since
$$\mathrm{SL}_2(\mathbb{Z})\cap \mathrm{SO}_2({\mathbb{R}}) = \left\{
\begin{bmatrix}\pm 1 & 0\\0&\pm 1\end{bmatrix},
\begin{bmatrix}0 & \pm 1\\\mp 1 & 0\end{bmatrix}
\right\},$$
the image of $\mathrm{PSL}_2(\mathbb{Z})$ in $\mathbb{H}^2$ is almost a Cayley graph, except for the fact that order-$2$ loops collapse, as seen in the following graph:
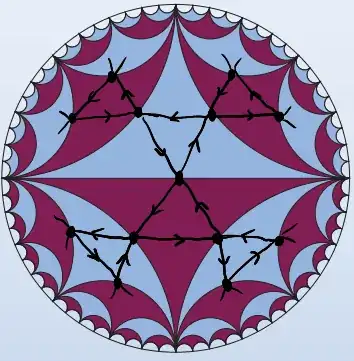
Even so, the symmetry group of the resulting graph in $\mathbb{H}^2$ is $\mathrm{PSL}_2(\mathbb{Z})$. It's possible to make a graph with this property with fewer edges by placing a single vertex in the center of each triangle then connecting them by an unorienteded edge across each edge of the triangle---that is, take graph that is dual to the triangulation.
In 1914, Max Dehn showed that trefoil knots are chiral. What he basically did was to look at the outer automorphism group of the fundamental group of a trefoil knot by analyzing what such a homomorphism would do to the Cayley graph. One of the steps was to quotient out by the center and analyze outer automorphisms of $\mathrm{PSL}_2(\mathbb{Z})$ by looking at what they would do to above sort of graph in $\mathbb{H}^2$, utilizing hyperbolic geometry. (Interestingly, he did not use an embedding in $\widetilde{\mathrm{SL}_2(\mathbb{R})}$, but rather an embedding into $\mathbb{H}^2\times \mathbb{R}$. Apparently non-compact manifolds have an ambiguity for which geometry it has. The trefoil complement also has a $\mathbb{H}^2\times \mathbb{R}$ geometry, and when Dehn considers the flattened Cayley graph in $\mathbb{H}^2$, it is using the obvious projection.)
See https://math.stackexchange.com/a/2511821/172988 for a summary and references.
