Question
Let $n$ be a number with $d\ge9$ digits when written in number base $b\ge2$.
Can $n$ be $3$-palindromic? That is, does there exist $b$, such that $n$ is simultaneously a palindrome in number bases $b,b+1,b+2$?
Below I will present solutions for $d=3,5,7$ (Each case has infinitely many solutions). I'm not sure whether the smallest solution for $d=9$ is very large, or does not exist for some unexpected reason.
I have confirmed my families of solutions for $d=3,5$ with an OEIS entry (link below). I have later, discovered seven more solution families, now for $d=7$, but I can't find a single solution example for $d\ge9$ (details below), still (For $d=9$, smallest example is $\gt10^{17}$, if it exists).
If all $3$-palindromes are found/characterized, then it would be easy to see whether any of them can exist as a part of a $4$-palindrome, whose existence is a open problem.
$3$-palindromic
A number $n$ is palindromic (a palindrome) in number base $b\gt1$ if it is the same when its digits are reversed in that number base. For example:
$121$ is a a palindrome in number base $10$ since $121=\color{}1\cdot10^2+2\cdot10^1+1\cdot10^0=121_{10}$
$5$ is a palindrome in number base $2$ (binary) since $5=\color{}1\cdot2^2+0\cdot2^1+1\cdot2^0=101_2$
I say that a number $n$ is $3$-palindromic if it is simultaneously palindromic in three consecutive number bases $b,b+1,b+2$, and has at least two digits in all of those number bases (Since one digit numbers are trivially palindromic). For example:
$178$ is $3$-palindromic since $178=454_6 = 343_7 = 262_8$ is palindromic in bases $6,7,8$.
$3360633$ is $3$-palindromic since $6281826_9=3360633_{10}=1995991_{11}$.
There are infinitely many "short enough" $3$-palindromes
Let $d$ be the number of digits a number $n$ has when written in base $b$.
If $d$ is small enough (numbers are "short enough"), and odd, we can find many examples:
There are no $3$-palindromes among $d$ digit numbers when $d$ is even. This is because when a number is a palindrome in base $b$, and also has an even number of digits in that base, then it is divisible by $b+1$ and thus ends with $0$ in base $b+1$.
Thus, lets assume $d$ is odd, and also $d\gt1$ since one digit numbers are trivially palindromic.
There are infinitely many numbers that are $3$-palindromic and have $d=3,5,7$ digits:
$178, 300, 373, 676, 1111, 1702, \dots$ are $d=3$ digit $3$-palindromes.
$154593982, 234531337, 344570692,\dots$ are $d=5$ digit $3$-palindromes.
$3360633, 19987816, 43443858,\dots$ are $d=7$ digit $3$-palindromes.
Characterization of all "short enough" $3$-palindromes $(d\lt 9)$
Formulas for above sequences are shown in comments of A279093, and here in more detail:
All numbers $n$ palindromic in number bases $b,b+1,b+2$ with $d=3$ digits are given by:
$F_3=\{n\in\mathbb N : n=\frac12(b^3 + 3b^2+5b+2),b=6+2k,k\in\mathbb N_0\}\cup\{300\}$
It can be proven$^{[1]}$ that $n$ is a $d=3$ digit $3$-palindrome if and only if $n\in F_3$.
All numbers $n$ palindromic in number bases $b,b+1,b+2$ with $d=5$ digits are in:
$F_5=\{n\in\mathbb N : n=\frac14(3 b^5 + 15 b^4 + 35 b^3 + 45 b^2 + 37 b + 13),b=45+4k,k\in\mathbb N_0\}$
I strongly conjecture that $n$ is a $d=5$ digit $3$-palindrome if and only if $n\in F_5$.
I conjecture that all $3$-palindormes with $d=7$ digits are given by:
$F_7=F^{(0)}_7\bigcup F^{(1)}_7\bigcup F^{(2)}_7\bigcup \dots \bigcup F^{(m)}_7\bigcup \dots$
Where sets $F^{(m)}_7,m\in\mathbb N$ are mutually disjoint and given by: $\{n\in\mathbb N : n=n_{m}(b)\}$, where $n_m(b)$ is a polynomial of degree $7$, that goes over $b=c+tk,c,t\in\mathbb N$, and where set $F^{(0)}_7$ is finite and already fully found (exact elements for $m=0$ can be found at the linked question or at the linked OEIS sequence, among "known terms that do not belong to any families").
I have found $F^{(m)}_7$ for $m=1,2,3,4,5,6,7$, and I think there could be more of these. The latest one has the smallest element of size $\approx 10^{17}$, and I haven't searched beyond $10^{18}$.
$F^{(m)}_7=\{n\in\mathbb N : n=n_{m}(b), b=c+tk, k\in\mathbb N_0\}$ then $[m, n_m(b), (c,t)]$ are given by:
(Where + sign should stand between the coefficients - but table is too wide then.)
$$ \begin{matrix} 1, & \frac12 ( 6 & 25 b & 55 b^2 & 73 b^3 & 55 b^4 & 25 b^5 & 7 b^6 & b^7 ), & (74,2)\\ 2, & \frac{1}{6} (4 & 25 b & 55 b^2 & 73 b^3 & 55 b^4 & 25 b^5 & 7 b^6 & b^7), & (56, 6) \\ 3, & \frac16(28 & 94 b & 175 b^2 & 217 b^3 & 175 b^4 & 91 b^5 & 28 b^6 & 4 b^7), & (173,6) \\ 4, & \frac{1}{6} (32 & 125 b & 275 b^2 & 365 b^3 & 275 b^4 & 125 b^5 & 35 b^6 & 5 b^7), & (278, 6) \\ 5, & \frac{1}{12} (10 & 68 b & 193 b^2 & 269 b^3 & 187 b^4 & 71 b^5 & 16 b^6 & 2 b^7), &(37,12) \\ 6, & \frac{1}{12} (66 & 256 b & 543 b^2 & 703 b^3 & 537 b^4 & 253 b^5 & 72 b^6 & 10 b^7), &(117,12) \\ 7, & \frac{1}{12} (10 & 80 b & 283 b^2 & 419 b^3 & 277 b^4 & 89 b^5 & 16 b^6 & 2 b^7), &(289,12) \end{matrix} $$
Notice that $c\equiv 2,5,2\pmod 6$ for $t=6$ and that $c\equiv 1,9,1\pmod {12}$ for $t=12$.
Also notice the unexpected coincidental similarity between $m=1,2$.
If you want to sort them by smallest element $\min\{F^{(m)}_7\}$, ascending, they would be in order: $m=5,2,1,6,3,7,4$, with those minimal elements being:
$$\begin{matrix} m & \min\{F^{(m)}_7\} & (b,b+1,b+2) \\ 5 & 19683596522 & (37,38,39) \\ 2 & 326217315210 & (56,57,58) \\ 1 & 6678940007962 & (74,75,76) \\ 6 & 265965216105640 & (117,118,119) \\ 3 & 3219426999580862 & (173,174,185) \\ 7 & 28854914566144178 & (289,290,291) \\ 4 & 109665618707825827 & (278,279,280) \end{matrix}$$
The next set, $F^{(8)}_7$ has smallest element $\gt 10^{18}$. I'm not sure how to find the next set, without the brute force search. There are probably more sets with both $t=6$ and $t=12$, and I'm not sure about $t=2$.
Q: Can we find a general characterization for sets $F^{(m)}_7$ (how many more are there)?
Update: Number bases $\le412$ and from $600$ to $612$ do not have a new solution (family). This indicates a new family of solutions, if it exists, would appear in bases $\gt 612$. Given first $7$ families appear in first $300$ bases, and in next $300$ bases no new families appear, it could be that the $8$th family does not exits.
Here you can see the seven known familis in more detail. (Exact digits in each base).
"Long numbers" as $3$-palindromes
Let $d\ge9$ be the number of digits of number $n$ when written in number base $b$, and let $n$ satisfy being a $3$-palindrome: Being palindromic in bases $b,b+1,b+2$.
I have no examples in this case.
They are either very large, or do not exist for some unexpected reason.
I have searched for the smallest example for $F_9$, and it has to be $\gt 10^{17}$, so far.
Haven't searched significantly in cases $F_d,d\ge 11$.
Q: Can we provide arguments why they would (not) exist?
I'm not sure how can one attempt to search for these solutions other than filtering out generated palindromes - there should be a better way, since the solutions for $d=3,5,7$ are very nicely characterized by $F_3,F_5,F_7$, and $d\ge9$ should follow similarly?
Q: How efficiently can we search/solve for elements in $F_d,d\ge9$?
$[1]:$ Proof for $F_3$, the $d=3$ digit $3$-palindromes
I believe I was able to show that $F_3$ contains all solutions for $d=3$. But I haven't been able to fully analyze $d=5,7,9$ in a similar way. The idea is in short simple and natural:
All palindromes with three digits are given with $Ab^2+Bb+A$ where $A,B<b$.
We can rewrite that as: $A(b+1)^2+(B-2A)(b+1)+(2A-B)$,
Now we can search for $2$-palindromes first, numbers palindromic in bases $b,b+1$:
We need now to satisfy (looking at digits of the rewritten expression):
$$1\le A-\alpha_1\le b$$ $$0\le B-2A +\alpha_1 (b+1) -\alpha_2 \le b$$ $$1\le 2A-B +\alpha_2 (b+1) \le b$$ To have a valid number, and to have a valid palindrome in base $b+1$: $$A-\alpha_1=2A-B+\alpha_2 (b+1)$$ Where $\alpha_1,\alpha_2\in\mathbb Z$ are freely used to "borrow" from and to neighbouring digits, to satisfy the first three conditions depending on $b,A,B$.
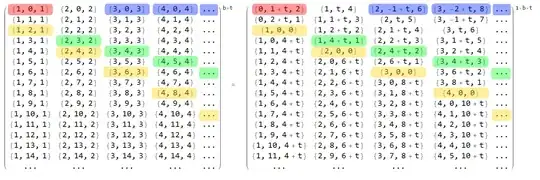
We can parametrize then all the $3$-digit numbers in base $b+1$ with some $t\in\mathbb N$:
(After preforming the trivial borrowing, we are observing bases $b+t,b+t+1$)
(Omitted the new $\alpha_1,\alpha_2$ gotten after trivial borrowing, from expressions, for readability)
And after this, we can show that the numbers on and below yellow line can't give base $b+1$ palindromes, and after further analysis and playing with conditions, one can show that $3$-palindromes must be numbers of forms located on green and blue lines.
Now we do the same thing, but for $b+1,b+2$ and considering only the blue and green forms, and after final analysis, one can finally prove and show that $F_3$ contains all $d=3$ digit $3$-palindromes, and that $d=3$ digit $4$-palindromes do not exist.
More specifically, the blue forms yield solution $300$ (see $F_3$), and the green forms yield the solutions generated by $b_3(b)$ that makes up the rest of $F_3$.
Q: Can we apply similar analysis to $d=5,7,9,\dots$ and solve/prove $F_d$?
A: I asked this question some time ago here. - not answered. Here you can also see this proof in more detail.
My poof for $d=3$ relied on guessing the right cases to split the parameterized forms into, and then solving each of those cases, splitting into subcases if necessary, until the proof contained all parameterized forms.
I wasn't able to guess $d=5$ cases that would allow the parameterized forms to be analyzed and $F_5$ found. Notice that if we were to use a similar image as above for form visualization, to help us guess the cases to analyze, we would now have for $d=5$, a 3-dimensional matrix of parameterized forms with $t$, and $\alpha_1,\alpha_2,\alpha_3,\alpha_4$ parameters.
I'm not sure how to transform this into a rigorous method to allow me to attack $d=5,7,9,\dots$
Clarification: If you can provide insight into $d\le 9$, then refer to the linked question. If you can provide insight into $d\ge 9$ and $d=7$ regarding $F_7^{(m)}$ for $m\gt7$, refer to this question.