Update: The following question answers the concerns in this question.
The linked question deals with the equivalent $b\to b-1$ approach instead of the $b\to b+1$ approach presented here, with more detail and being clearer, and makes everything here obsolete regards to solving this particular problem.
I advise you to visit that linked question instead, if you came here for Palindromes in three consecutive bases problem.
However, if you still want to deal with the $b\to b+1$ approach specifically, which is having much harder time to accomplish the same effects as the linked question already did, then this is the question you can read.
To Summarize Why: The reason why $b,b-1$ is better than $b,b+1$ is that we avoid negative digits in non-normalized forms, in the context of this question. - Or equivalently, in the context of the linked question, we can use non-negative $o_i$ parameters only instead of needing to handle $o_i\in\mathbb Z$. I also would like to thank user Grešnik for discussing this problem and such alternative approaches with me.
Summary
I do not know how to solve the problem of finding all numbers palindromic in three consecutive number bases generally,
I've since split it into countably many subproblems, each asking to find all $d$ digit numbers palindromic in three consecutive integer number bases.
I've been computing the solutions for first four subproblems (digit cases $d=3,5,7,9$), but such progress reached the point of requiring too much time to reveal the next solution.
Problem
Is there a better way to solving the problem than the one presented below?
Is it possible to use a computer to solve individual cases of $d$ in a similar way that I did for $d=3$ by hand? To work out the inequalities and all the absolute forms?
Or can the presented method perhaps be fine tuned and then used effecitvely?
All in all, what's the best course of action to take for solving this problem further?
Notation
I'll be using the notation (definition):
$$N=\sum_{i=0}^{n} a_ix^i=(a_n,a_{n-1},\dots,a_1,a_0)_x$$
To represent the natural number $N$ in natural number base $x\ge2$ with digits $a_n,\dots,a_0$.
If digits are "valid", that is they are $\in\mathbb N_0$, and $a_i\lt x,\forall i$ and $a_n\ne 0$, then the representation is unique. Let this unique representation of some number $N$ be called "the absolute (true) representation" of $N$ in number base $x$.
For example, $100=(1,0,0)_{10}=(1,2,1)_9=(1,2,1,0)_4=(5,15)_{17}=(6,10)_{15}$
Or for example, how is number $16$ wrtten in binary? $16=(1,0,0,0,0)_2$ would be the true (the absolute) representation.
Let's allow non-absolute representations, by allowing that the digits are $\in\mathbb Z$. Then we can have for example $100=(1,-2,1)_{11}$. Every non-absolute representation can be converted to the unique absolute one. In this case, we see that the second digit is $\lt0$ so we borrow from the first digit and we have (from the definition):
$$100=(1,-2,1)_{11}=(1-1,-2+11,1)_{11}=(0,9,1)_{11}=(9,1)_{11}$$
Which is now the true representation.
The borrowing is usually done forward or backwards between two neighbouring digits:
$$(a_n,\dots,a_i,a_{i-1},\dots,a_0)_x=(a_n,\dots,a_i\pm\alpha,a_{i-1}\mp\alpha x,\dots,a_0)_x, \text{ } \alpha\in\mathbb N$$
Depending if the irregular digit is negative or exceeding the number base.
A number is palindromic in base $x$ if its absolute representation in that base is palindromic: $a_{n-i}=a_{i},\forall i$.
The general problem
How to find all numbers that are simultaneously palindromic in multiple number bases?
(I'm not considering trivial one digit palindromes.)
I'm mainly interested in the subproblem of consecutive number bases.
For example, the smallest number palindromic in three consecutive number bases:
$$178 = (1,7,8)_{10} = (4,5,4)_6 = (3,4,3)_7 = (2,6,2)_8$$
My approach for solving the problem in question
I'm mainly interested in numbers palindromic in consecutive integer number bases; which is the problem in question.
Instead of looking at all the numbers at once, I've decided to solve for $d$ digit palindromes. That is, split the problem in question, to countably many subproblems and attempt to solve each one individually, as I do not know how to approach this generally.
That is, my problem becomes: given $d\gt1$, how to find all numbers that are $d$ digit palindromes (Having $d$ digits in base $x$) when written in the consecutive integer number bases $x,x+1,x+2,\dots,x+k$, where $k\ge2$?
If a number is palindromic in consecutive $b$ number bases with $d\gt1$ digits in those bases, then I call it a $b$-palindrome. Notice that if a number isn't a $b$-palindrome, then it can't be a $(b+1)$-palindrome or higher. Similarly, a $b$-palindrome is also a $(b-1)$-palindrome. A $1$-palindrome is simply a number which is palindromic in at least one number base with $d\gt1$ digits.
Notice that there are no solutions for even cases of $d$. This is because a number that is a even length palindrome in number base $x$, is divisible by $x+1$, and thus cannot be palindromic in base $x+1$, hence it cannot be a $2$-palindrome or higher. Note: It can happen for example that a odd palindrome in base $x$ is even palindrome in base $x+1$, for example $10=(1,0,1)_3=(2,2)_4$.
Thus, we can only consider odd cases of $d=3,5,7,9,11,\dots$
That is, from now on, $d=2r+1, r\in\mathbb N$.
Let's denote:
- with $f_d$ a set of all $d$ digit $2$-palindromes
- with $F_d$ a set of all $d$ digit $3$-palindromes
- with $\mathcal F_d$ a set of all $d$ digit $4$-palindromes.
Conjectures:
- $f_d\ne\emptyset$ for all $d$.
- $\mathcal F_d=\emptyset$ for all $d$.
Finally, the stated problem I want to solve:
How to find $F_d$ for all $d$?
Solving the first case, $d=3$ :
Solution: All numbers $n$ palindromic in number bases $x,x+1,x+2$ with $3$ digits are given by:
$$F_3=\{n\in\mathbb N : n=\frac12(x^3 + 3x^2+5x+2),x=6+2r,r\in\mathbb N_0\}\cup\{300\}$$
Where $x=7$ for the rouge $n=300$ solution.
Proof: (Visualization included at the end.)
We need to prove that there are no other solutions.
We'll also rediscover the above solutions in the process.
To find $F_3$ solutions, first we find $f_3$ solutions and then check them for the third consecutive base.
It holds by definition:
$$N=(a,b,a)_x=(a_0,b_0,c_0)_{x+1}=(a,-2a+b,2a-b)_{x+1}$$
Where we would want $x=\max\{a,b\}+t,t\in\mathbb N$ so that at least $(a,b,a)_x$ is an absolute representation.
In case you don't see the above equality:
$$\begin{align} N&=(a,b,a)_x\\&=ax^2+bx+a\\&=x((x+1)-1)^2+b((x+1)-1)+a\\&=a(x+1)^2+(-2a+b)(x+1)+(2a-b)\\&=(a,-2a+b,2a-b)_{x+1} \end{align}$$
Now we need to find all $a,b$ such that $a_0=c_0$, where $a_0,c_0$ are written as digits of the absolute representation of the number $N$ in base $x+1$. Notice that the above representation $a_0=a,c_0=2a-b$ is not necessarily absolute. To be able to work with absolute representations, we need to split this into cases.
Case $(-2a+b\gt0)$:
We can write $b=2a+\alpha,\alpha\in\mathbb N$. Then we have:
$$N=(a,b,a)_x=(a,-2a+b,2a-b)_{x+1}=(a,\alpha,-\alpha)_{x+1}=(a,\alpha-1,-\alpha+x+1)_{x+1}$$
Then substitute $x=\max\{a,b\}+t=b+t=2a+\alpha+t$:
$$(a,\alpha-1,-\alpha+x+1)_{x+1}=(a,\alpha-1,2a+t)_{2a+\alpha+1+t}$$
Which is now clearly seen to be the absolute representation of $N$ for this case.
Now we can observe $a_0=c_0$ and clearly see that $a=2a+t\implies a=-t$ is a contradiction since $(a,b,a)_x$ wouldn't be an absolute representation then, thus we do not have any $f_3$ solutions for this case, which also means we do not have any $F_3$ solutions for this case.
Case $(-2a+b=0)$:
$$N=(a,b,a)_x=(a,-2a+b,2a-b)_{x+1}=(a,0,0)_{x+1}$$
Where the last step is clearly an absolute representation, and clearly not a palindrome, thus we do not have any solutions for this case either.
Case $(-2a+b\lt0)$:
$$N=(a,b,a)_x=(a,-2a+b,2a-b)_{x+1}=(a-1,-2a+b+x+1,2a-b)_{x+1}$$
Now to get an absolute representation out of this, I find it easier to split into subcases $i)$ and $ii)$:
$i)\text{ }2a\gt b\ge a$ :
We can write $b=a+\alpha_0,\alpha_0\lt a,\alpha_0\in\mathbb N_0$, and we have $x=a+\alpha_0+t$, then we can substitute this:
$$(a-1,-2a+b+x+1,2a-b)_{x+1}=(a-1,2\alpha_0+1+t,a-\alpha_0)_{a+\alpha_0+1+t}$$
And see we do have an absolute representation. Then we can observe: $$a_0=c_0\implies a-1=a-\alpha_0\implies\alpha_0=1$$
From which it follows:
$$(a-1,2\alpha_0+1,a-\alpha_0)_{a+\alpha_0+1+t}=(a-1,3+t,a-1)_{a+t+2}$$
The rightmost expression is clearly a palindromic absolute representation in base $x+1$. This gives us $f_3$ solutions for this case if we observe the absolute representations:
$$(a,a+1,a)_{a+t+1}=(a-1,3+t,a-1)_{a+t+2}$$
Now we need to check them in the third consecutive base $x+2=a+t+3$:
$$ N=(a,-4a+b,5a-2b)_{x+2}=(a,-3a+1,3a-2)_{a+t+3}$$
We need to find $a,t$ such that the absolute representation of $N$ in base $x+2$ is palindromic.
We need to play with $x+2$ representation to reach an absolute one. Lets start by borrowing two times from first to second, and once from third to first digit:
$$ (a,-3a+1,3a-2)_{a+t+3} = (a-2,-a+8+2t,2a-5-t)_{a+t+3} $$
Now in first part we assume: $a\ge2t+8\implies a=2t+8+\alpha_0,\alpha_0\in\mathbb N_0$.
From which we reach an absolute form that yields a contradiction:
$$(a-2,-a+8+2t,2a-5-t)_{a+t+3}\\= (2t+6+\alpha_0,-\alpha_0,3t+11+2\alpha_0)_{3t+11+\alpha_0}\\= (2t+5+\alpha_0,3t+11,\alpha_0)_{3t+11+\alpha_0}$$
$$\implies 2t+5+\alpha_0=\alpha_0 \implies t=-5/2, \text{contradiction.}$$
Which means this assumption does not have solutions in $F_3$ under this case.
Which leaves us to consider: $a\lt 2t+8$, which leaves us with an absolute representation:
$$ (a-2,-a+8+2t,2a-5-t)_{a+t+3} $$
Where we have: $a-2=2a-5-t\implies t=a-3$ Which means we actually have:
$$ (a-2,-a+8+2t,2a-5-t)_{a+t+3}=(a-2,a+2,a-2)_{2a},a\ge 3$$
Which does give solutions for $F_3$ under this case. We have:
$$N=(a,a+1,a)_{2a-2}=(a-1,a,a-1)_{2a-1}=(a-2,a+2,a-2)_{2a}$$
Note that $a\ge4$ for the first expression to remain in absolute form.
Now we've covered all of case $i)$ and have found $F_3$ solutions in all bases $x=2(4+r)-2=6+2r,r\in\mathbb N_0$ of form:
$$N=(a,a+1,a)_{2a-2}=a(2a-2)^2+(a+1)(2a-2)+a=\frac12(x^3 + 3 x^2 + 5 x + 2)$$
Now all that's left to check is the following case for the remaining solutions:
$ii)\text{ }b\lt a$ :
$$(a,-2a+b,2a-b)_{a+t+1}=(a-1,-a+b+t+1,2a-b)_{a+t+1}$$
Now if we assume that $t$ is large enough, that is,$2a-b\lt a+t+1$, then we only need to fix the middle digit to bring the expression to absolute form, with some $\alpha_0\in\mathbb N$, which means that if $t$ is large enough, we need to satisfy $a-1-\alpha_0=2a-b$ for solutions, which is clearly false.
This implies that if there are solutions for this case, then $2a-b\ge a+t+1 \implies t\lt a-b$,
$$(a-1,-a+b+t+1,2a-b)_{a+t+1}=(a-1,-a+b+t+2,a-b-t-1)_{a+t+1}$$
If we substitute: $t=a-b-T,T\in\mathbb N, T\lt a-b$ we have the above expression equal:
$$(a-1,-T+2,T-1)_{2a-b-T+1},a\ge2$$
If $T<3$ then we have a absolute form, so $a-1=T-1\implies a=T\implies a=T=2$
And if we look at the base $2a-b-T+1=3-b$ we see that it must be $b=0$, and that the base is $3$. This means $t=0$, which is a contradiction, thus we do not have a solution if $T<3$.
Otherwise, if $a-b\gt T\ge3$, we then have $a-2=T-1\implies t=1-b\implies b=0,t=1$, and we are left with:
$$N=(a,0,a)_{a+1}=(a-2, 5, a-2)_{a+2},a\ge3$$
Which gives the remaining solutions for $f_3$. Now we check them for remaining solutions for $F_3$:
$$(a,-4a+b,5a-2b)_{x+2}=(a,-4a,5a)_{a+3}=(a-3,-a+12,2a-9)_{a+3}$$
Now if $a\ge12$ then we have: $(a-3,-a+12,2a-9)_{a+3}=(a-4,16,a-12)_{a+3}$ which is never a palindrome. Else, if $a\lt12$, then the only solution is $a-3=2a-9\implies a=6$.
This gives a solution for $F_3$ which equals:
$$(3,6,3)_9=(4,5,4)_8=(6,0,6)_7=300$$
And we've with this last check finished checking case $ii)$, which was the last one.
This ends the proof.
Notice we haven't considered the case when the $x+1$ representation has a absolute form of $d-1$ digits, which can indeed happen for small enough $a,b$.
Such $f$ solution will be then divisible by $x+2$ ($N$ would be even length palindrome in base $x+1$) and thus will not be a solution for $F$.
Just for completion, the only $f_3$ solution for this case is $10=(1,0,1)_3=(2,2)_4=(2,0)_5$, not being $F_3$ solution as it is divisible by $5$ and thus not palindromic in the third consecutive base.
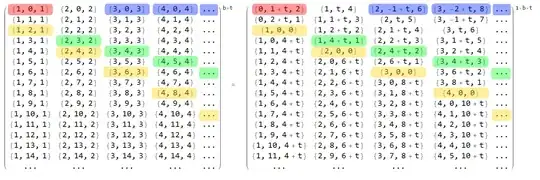
Proof Visualization
Where the first matrix represents $(a,b,a)_{B+t}$ forms as elements, and the second matrix represents those forms in base $B+t+1$. (Where $B$ is the smallest base so that the absolute forms make sense.)
Colored in yellow is the case $b=2a$ from the proof, above it are the third case, and below it are the first case elements.
Colored in green is the first set of $f_3$ solutions we find in the proof, and colored in blue is the second set of $f_3$ solutions we find in the proof.
Looking at green examples, you can see in the right table that the form is absolute and they're clearly $f_3$ solutions. Looking at blue examples, you can see that we do not have a direct absolute form. That's why we needed to go into more subcases and consider what happens when number base is or is not large enough.
Colored red is the only "unimportant" $f_3$ solution, the $10=(1,0,1)_3=(2,2)_4$ that obviously does not extend to $F_3$.
Then to extend $f_3$ to $F_3$, we observe the third table (that is not included) for base $B+t+2$.
$$ *** $$
To visualize $d=5$ in the same way, we would need a three dimensional matrix. For $d=7$, a four dimensional matrix, for $d=9$, a five dimensional matrix, and so on.
I'm not sure how can I visualize this better and use it to help me find absolute forms and candidates for solutions for $d\ge5$ like I did for $d=3$?
Solving the second case, $d=5$ :
Solution: All numbers $n$ palindromic in number bases $x,x+1,x+2$ with $5$ digits are given by:
$$F_5=\{n\in\mathbb N : n=\frac14(3 x^5 + 15 x^4 + 35 x^3 + 45 x^2 + 37 x + 13),x=45+4r,r\in\mathbb N_0\}$$
Proof:
$$***$$
The idea is the same as the $d=3$ case, split it smartly into cases to isolate absolute forms and check whether they are $2$-palindromic, and then among them check which extend to $3$-palindromic.
But I haven't yet completed this proof: It seems impractical to apply here the same exhaustive procedure that was applied for the smallest case of $d$; as I'm ending up spending too much paper, without managing to reach the end of it.
And that's why I'm posting this question here:
Can proofs for individual $d$ be done more efficiently? Using a better approach or fine tuning the current method? Perhaps, it it possible to use a computer to resolve the proof?
Solving the third case, $d=7$ :
Computations so far: I've got seven unique sets of countably many solutions, each generated by a polynomial expression; and twelve rouge solutions not falling into any sets of solutions.
I suspect there are possibly more sets, as the latest set has the smallest element $\gt10^{17}$, and I haven't gone beyond $10^{18}$ yet.
At this point, I don't think searching by computation more solutions is worth it.
A proof like for the first case of $d$ should be formulated to find all solutions; But the problem is, that I'm not sure how to do it efficiently, or even if I would be able to complete the full proof if I followed the same idea from the first case of $d$. (Since I'm already stuck on fully fleshing out $d=5$ solutions proof.)
So far, I have that $F_7$ equals the union of the following sets ($n\in\mathbb N,r\in\mathbb N_0$):
$$\{n=\frac{1}{2} (6 + 25 x + 55 x^2 + 73 x^3 + 55 x^4 + 25 x^5 + 7 x^6 + x^7):x=74+2r\}$$ $$\{n=\frac{1}{6} (4 + 25 x + 55 x^2 + 73 x^3 + 55 x^4 + 25 x^5 + 7 x^6 + x^7):x=56+6r\}$$ $$\{n=\frac16(28 + 94 x + 175 x^2 + 217 x^3 + 175 x^4 + 91 x^5 + 28 x^6 + 4 x^7) ,x=178+6r\}$$ $$\{n=\frac{1}{6} (32 + 125 x + 275 x^2 + 365 x^3 + 275 x^4 + 125 x^5 + 35 x^6 + 5 x^7):x=278+6r\}$$ $$\{n=\frac{1}{12} (10 + 68 x + 193 x^2 + 269 x^3 + 187 x^4 + 71 x^5 + 16 x^6 + 2 x^7),x=37+12r\}$$ $$\{n=\frac{1}{12} (66 + 256 x + 543 x^2 + 703 x^3 + 537 x^4 + 253 x^5 + 72 x^6 + 10 x^7),x=117+12r\}$$ $$\{n=\frac{1}{12} (10 + 80 x + 283 x^2 + 419 x^3 + 277 x^4 + 89 x^5 + 16 x^6 + 2 x^7),x=289+12r\}$$ $$\{3360633,19987816,43443858 ,532083314 , 1778140759 ,2721194733 ,11325719295 ,47622367425 , 97638433343 ,224678540182 ,265282702996 ,561091062285\}$$
Solving the fourth case, $d=9$ :
Computations so far: No examples exist in first $100$ number bases, and no examples of magnitude $\le 10^{18}$ have been found in first $150$ number bases. This implies the smallest example for $F_9$, if it exists, is at least $\gt 10^{17}$.
$$***$$
Solving the general case, $F_d$ :
Is it possible to solve this generally? Find all $F_d$ sets?
To generally solve this is a stretch I'm not expecting to be accomplished.
Any ways to acquire more solution for more cases of $d$ would help a lot; Although my main question here is if and how can one efficiently find (prove) all solutions for arbitrary cases of $d$, like it was done with $d=3$?
Relevant questions (Mostly just mentions of computed data as they predate $F_3$ proof):
Finding palindromes in two bases, specifically, $f_9=?$: (x,x+1), main interest in $d=9$?
Alternative to finding $f_d$ and using it to find $F_d$ is: finding $f'_d$ which is a set of all numbers palindromic in bases $x,x+2$: Computation patterns for (x,x+2) for small $d$.
Is $\mathcal F_d$ really empty for all $d$? $\mathcal F_d=\{?\}$, for any $d$?
Idea on proving $\mathcal F_d=\emptyset,\forall d$ by proving claims $(1)$ and $(*)$ - The $(1)$ from that post can be easily proven now by extending the proof of $d=3$ here to observe the base $x+3$. To prove $(*)$, one would need to generally consider $F'_d$ - sets of $d$ digit palindromes in bases $x$ and $x+3$ and ($x+1$ or $x+2$).