How many quotients/remainders can we get for a given Gaussian integer?

Question

This is a question which arose¹ from division of Gaussian integers. However, it seems to be basically a question about lattices in $\mathbb R^2$.

We know that if we consider $\mathbb Z[i]=\{a+bi; a,b\in\mathbb Z\}$ then we have a division with remainder, that is, for any $a,b\in\mathbb Z[i]$ with $b\ne 0$ there exist a quotient $q$ and a remainder $r$ such that $$a=qb+r, \qquad |r|<|b|.\tag{1}$$ This is basically the statement that $\mathbb Z[i]$ is an Euclidean domain (with norm $N(z)=|z|^2$).

The equation $(1)$ is equivalent to $$\frac ab=q+\frac rb, \qquad \left|\frac rb\right| <1. \tag{2}$$ So we are basically asking whether for a given complex number (in fact, a Gaussian rational) $\frac ab$ there is a Gaussian integer with distance at most one.²

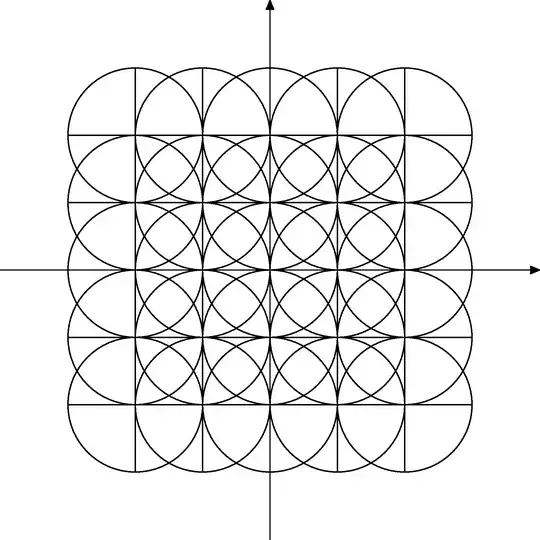
The following picture shows circles with radius one around each lattice point from $\mathbb Z[i]$, to find $q$ we basically check whether $\frac rb$ belongs to one of these circles.

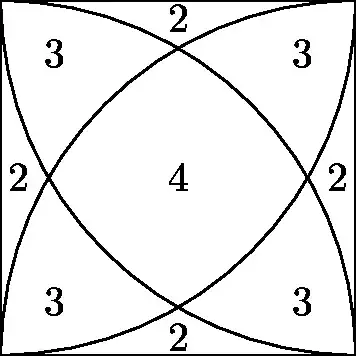
We can see that the $q$ is not necessarily uniquely determined. Depending on the position of $\frac rb$ in the squares determined by $\mathbb Z[i]$ we can have up to four possibilities.

Question. For a given $b\in\mathbb Z[i]$, what are the numbers of possibilities we can get for $q$? For example, what is the characterization of $b$'s such that, depending on $a$, we can have either one or four possible choices for $q$ in $(1)$? What is the characterization of $b$'s such that for some $a$'s we might have only one choice, for other $a$'s we can get two choices, and there are also $a$'s with for possible choices for $q$? What are $b$'s such that (depending on $a$) we might get one, two, three or four choices for $b$?

If we look at the interpretation explained in $(2)$, we are basically asking whether there are linear combinations of $\frac1b$ and $\frac ib$ which belong to areas denoted by $1$, $2$, $3$, $4$ of some square in the grid.

Let us have a look at some special cases:

• If $r=0$, i.e. $\frac ab \in \mathbb Z[i]$, then there is only one possibility how to choose $q$. (And this is the only situation where we have single possibility.)
• Let us take $b=1-i$ for example, meaning that $\frac1b=\frac12(1+i)$. We see that any multiple of $\frac1b$ by a Gaussian integer is either in the center of some of the squares or in some of it's vertices. So we see that we always get one or four possible remainders. (For example, $1=0\cdot(1-i)+1=1\cdot(1-i)+i=i\cdot(1-i)-i=(1+i)\cdot(1-i)-1$.)
• If we take $b=2$, this corresponds to multiples of $\frac12$. So we get one, two or four possible remainders depending on $a$. (For $a=1$ we have two possibilities, $1=0\cdot2+1=1\cdot2-1$. For $a=1+i$ we have $1+i=0\cdot2+(1+i)=1\cdot2+(-1+i)=i\cdot2+(1-i)=(1+i)\cdot2+(-1-i)$.)
• It seems plausible that if $|b|$ is large enough (to make multiples of $1/|b|$ rather dense) and $b$ isn't in some of the special directions (such as multiples of $1$ or $1+i$ by some unit, i.e., by $\pm1$ or $\pm i$) then we can hit all possible areas and there will be $a$'s with one, two, three and four choices for $q$.
• If the intuition suggested in the previous bullet point is correct, it seems that there will be finitely many exceptions, but typically we should get all four possibilities. However, it does not seem to be quite straightforward to get some estimate on what "dense enough" and "special directions" should be in this context.
• Moreover, "dense enough" (as used in the previous bullet point) seems to be dependent on the direction of the vector corresponding to $\frac1b$. So it's quite possible that there is not some simple characterization - or that entirely different way of looking at the problem is needed.

¹I thought about this question after somebody recently asked in chat about non-uniqueness of division in Gaussian integers. (As they mentioned, they've stumbled upon a remark about this in Artin's algebra.)

²This is actually the approach usually taken in the proof, see: Prove that the Gaussian Integer's ring is a Euclidean domain

Answer 1

Following the advice in fedja's comment I have tried to look at the possibilities by "trial and error".

It seems that the Gaussian integers which do not admit all four cases (i.e., one, two, three or four possible remainders - depending on choice of $a$) are $$ \begin{array}{|c|c|} \hline 1 & 1 \\\hline 2,3 & 1,2,4 \\\hline 1+i & 1,4 \\\hline 1+2i,2+i & 1,3 \\\hline \end{array} $$ and the number associated with them (i.e., the numbers we get by multiplication by one of the units)

I believe the argument explained in the comment shows that we don't have to worry about $b$'s such that $|b|\ge7$.

The picture below shows where multiples of $\frac1b$ are located for $b=k+li$, $1\le k\le 6$ and $0\le l\le 5$.

This picture represents the multiples of $\frac1b$ by a Gaussian integer shifted into the fundamental square. I.e., if $z\in\mathbb Z[i]$ and $z\frac1b=x+iy$, then the point with the coordinates $(\{x\},\{y\})$ is displayed in the diagram. (Here $\{x\}$ denotes the fractional part of $x$.) The position of $\frac1b$ is marked as the red point.