1

Consider the following background information:

I have a sphere that equally divided in to two hemisphere P and S. There is a plane that separate two different zone. Upper zone called A and lower zone called B. The angle $\alpha$ defined where the sphere is touching the intersection plane. So $\alpha$ larger means sphere is more in zone A and vice versa. The angle $\beta$ defines the orientation of the sphere. Schematic representation of this is below.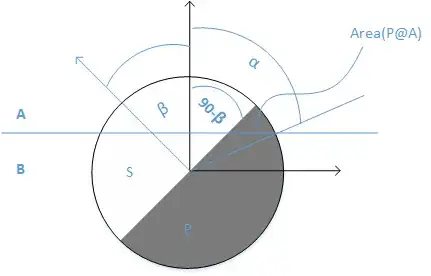enter image description here

To calculate the area of $P$ portion of the sphere into $A$ is given by following equation $$ \mathrm{Area}_{P-A}= r^2\int_{\theta=\frac{\pi}{2}-\beta}^\alpha \int_{\phi=\arcsin(1/(\tan\theta \tan \beta))} ^{\pi -\arcsin(1/(\tan\theta \tan \beta)} \sin\theta\; d\theta d\phi. $$

After solving this equation we can get the following solution. $$ \textrm{Area}_{P-A}= 2 r^2 \left\{ \cos (\alpha) \sin ^{-1}(\cot (\alpha) \cot (\beta)) -\tan ^{-1}\left(\frac{\cos (\beta)}{\sqrt{\sin ^2(\beta)-\cos ^2(\alpha)}}\right)\right\}+\pi r^2 (1-\cos (\alpha)). $$

Note that the solution is defined as a function of $\alpha$ and $\beta$. If we change the value of $\alpha $ and $\beta$, the area of P into A will change eventually.

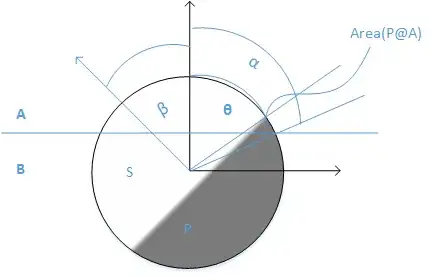
Now consider more complex case where $P$ and $S$ are not equal hemisphere. enter image description here

Question: If $P$ and $S$ are not equal, then what should I consider if I want to calculate the area of $P$ into $A$ as a function of $\alpha$ , $\theta$ and $\beta$? Here $\theta$ defines the distance of the cap edge from center.

Note:

I have seen this question:

Calculate the area on a sphere of the intersection of two spherical caps

where it solves for two spherical cap separate each other by an angle and calculate the area of their intersection. In my problem, I would like to calculate the area of one spherical cap when it cross a fixed intersection. I am looking for an analytical solution like the top one so that I can be able to calculate area when sphere going up and down and it rotate.

T. an
  • 159
  • In the first case, the area P spans an angle of 180°. What angle does it span in your second diagram? The answer is going to depend on it; for example, if the angle spanned is small enough, then the intersection between P and A will be empty. – Michael Seifert Jun 04 '19 at 12:08
  • As it is a dynamics situation I suppose to have a general solution like the first case where the area will be a function of alpha and beta. area will be valid for certain alpha and beta range. – T. an Jun 04 '19 at 12:14
  • @MichaelSeifert This is a unique problem. I do not think that it is a duplicate problem. Please check both problems. – T. an Jun 04 '19 at 12:16
  • My point is that alpha and beta aren't sufficient to determine the area. You'll need a third number to tell you how much of the sphere is covered by P before you can determine the area of the intersection between A and P. – Michael Seifert Jun 04 '19 at 12:17
  • In that case we can take h as the height of the cap. So the equation will also be a function of h. – T. an Jun 04 '19 at 12:19
  • 1
    @Xander Hendeson and others.. O do not know how it becomes duplicate and nobody can provide an exact answer for 5 days. Please read both post and give a specific answer. I clearly mention that I am looking for an analytical solution for my problem. I did not see any. – T. an Jun 06 '19 at 06:27
  • 1
    @Tanvir: Let me outline how the area you ask about might be realized as the intersection of two spherical caps. The hemisphere P is a spherical cap (a special kind of course), and the region A cut off by the plane is a spherical cap (this is by definition). Perhaps the proposed duplicate fails in your eyes because its solution is not sufficiently analytical? A little clarification on your part would be helpful. – hardmath Jun 06 '19 at 17:05
  • @hardmath Sir, Can you please tell what more clarification or information is necessary? I need an analytical solution as this problem is a continuous problem from part 1. Thats why I have to keep my expression using that one with only added any parameter for defining the position of spherical cap. – T. an Jun 06 '19 at 17:56
  • 2
    @Tanvir: When the problem is changed to replace the hemisphere with a smaller spherical cap, the generality is exactly as in the duplicate Question. The essential difference is how the figure is parameterized. Both Questions use $r$ for the radius of the sphere (although this appears only in your formulas, not in the exposition of your problem). Three more parameters are needed to pose the problem. Work out how to express the parameters of the other Question in terms of the ones you chose, and you'll have an Answer. – hardmath Jun 06 '19 at 22:40

0 Answers0