I am trying to understand construction of irreducible polynomial of odd degree over $\mathbb{Q}$ with exactly two non-real roots. Let $g(x)=(x^2+m)(x-n_1)\cdots (x-n_{k-2})$ with $m>0$, $n_1< \cdots < n_{k-2}$ and $k\ge 3$ odd.
(1) $n_1$ being simple simple root, $g'(n_1)\neq 0$, so in small neighbourhood of $n_1$, $g$ is either strictly increasing or decreasing. Assume first case is there [so from $n_1$ toward right, in small neighbourhood, $g$ is increasing.]
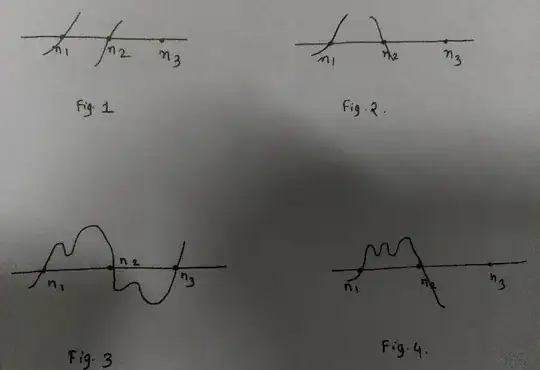
(2) If $g$ is strictly increasing in neighbourhood of $n_2$, then it is situation of Fig. 1 below. This will force $g$ to have one more root between $n_1$ and $n_2$. This is contradiction to the choice of $g$. [So Fig. 1 is impossible]
(3) Conclusion: If $g$ is strictly increasing in small neighbourhood of $n_1$ then it is strictly decreasing in small neighbourhood of next simple root $n_2$. So it is in Fig. 2. Moreover (this justification says that) if in $(n_1,n_2)$, $g$ has a relative maxima, then in next interval $(n_2,n_3)$ it must have a relative minima.
Q. Is it necessary that relative maxima/minima for $g$ above in any interval above is unique?
Partial answer: We can say that Fig. 3 and Fig. 4 should not occur. Suppose Fig. 3 is possibility. Notice that in $(n_1,n_2)$, $g'(x)$ has three zeros. [A point $a$ is local maxima or minima implies $g'(a)=0$].
If $a$ is local maxima/ minima, call it local extrema. We've $k-3$ intervals $(n_i,n_{i+1})$ for ($1\le i\le k-3$).
Then, the total extremas for $(k-3)$ intervals is $\ge (3) + (3) + (1+\cdots + 1) $ [with $1$ appearing $k-5$ times]. This is $k+1$, which is $>\deg(g'(x))$, contradiction. Similarly Fig. 4 is not possible.
So my question is about, precisely: In only one interval, say $(n_1,n_2)$ can $g$ have exactly three extrema?
Ref. Jacobson's Basic Algebra Vol. 1 (p. 269).