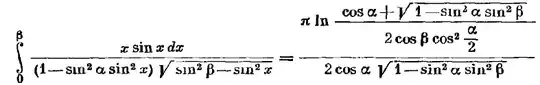19

This question at MathOverflow https://mathoverflow.net/questions/302982/how-to-prove-the-identity-l2-frac-cdot3-frac215-sum-limits-k-1-inf conjectures certain relation between fast converging hypergeometric series and Gieseking's constant Hypergeometric series for $\mathrm{Cl}_2(\pi/3)$ . This constant is the volume of the hyperbolic 3-manifold called Giesekings' manifold https://de.wikipedia.org/wiki/Gieseking-Konstante

The hypergeometric series under consideration has trigonometric integral representations, which give two different forms of the conjecture:

$$\int_0^{{\pi }/{3}} \frac{x \left({\sqrt{3}-{\sin x}}\right)\, dx}{\sin x \cdot \sqrt{3-2 \sqrt{3} \sin x}}\overset{?}{=}\frac{5}{2}\text{Im}\left(\text{Li}_2\left(e^{\frac{2 i \pi }{3}}\right)\right)\tag{1}$$

$$ \int_0^{{\pi }/{3}} P(x)\, \frac{xdx}{\sin x \sqrt{\frac{3}{4}-\sin ^2x}}\overset{?}{=}5 \sqrt[4]{3}\, \rm{Im}\left(\rm{Li}_2\left(e^{\frac{2 i \pi }{3}}\right)\right)\tag{2} $$

where,

$$P(x)=\left(\frac{\sqrt{3}}{2}-\sqrt{\frac{3}{4}-\sin ^2x}\right)^{3/2}+\left(\frac{\sqrt{3}}{2}+\sqrt{\frac{3}{4}-\sin ^2x}\right)^{3/2}$$ The 2nd represenation is interesting because Lobachevskii has studied similar integrals in relation to volumes in hyperbolic geometry in his work "Application of imaginary geometry to certain integrals" (1836). Also see equation 3.842.7 in Gradsteyn and Ryzhik. For example he proves the following integration formula

enter image description here

This formula in the limit $\alpha\to\pm i\infty $ becomes $$ \int_0^\beta\frac{xdx}{\sin{x}\sqrt{\sin^2{\beta}-\sin^2{x}}}=\frac{\pi}{4\sin{\beta}}\ln{\frac{1+\sin{\beta}}{1-\sin{\beta}}}.\tag{3} $$ One can see that when $\beta=\pi/3$, then both (2) and (3) have the same factor $\frac{x}{\sin{x}\sqrt{\sin^2{\beta}-\sin^2{x}}}$, and if it wasn't for the convoluted factor $P(x)$ these integrals would be the same.

Lobachevski studies other integrals and in particular shows that the integral with the variable upper limit $y<\beta$ $$ \int_0^y\frac{xdx}{\sin{x}\sqrt{\sin^2{\beta}-\sin^2{x}}} $$ can be expressed as a sum of elementary functions and Clausen functions.

Maybe (2) is related to hyperbolic geometry and there is certain substitution that can transform this integral into a sum of Clausen functions or maybe it has geometric interpretation?

Q: How to prove conjectures (1) and (2)?

Tito Piezas III
  • 54,565
Martin Nicholson
  • 3,883
  • The first integral is equal to $$\frac{10}{3} \int_0^{1/2} \frac{\sin^{-1} (t)}{t} dt$$ though I have obtained this integral from the hypergeometric form of the right hand side. It remains to prove that the two integrals are equal – Yuriy S Jun 11 '19 at 14:17
  • 1
    I would link this question as well – Yuriy S Jun 11 '19 at 14:48
  • @YuriyS: This new post would also be relevant. – Tito Piezas III Jun 12 '19 at 09:08
  • @Nemo: In this MO post, you converted a series into an integral. Can you do the reverse for the post above, namely convert the integral $(1)$ into a series? (The denominator involves the same factors.) – Tito Piezas III Jul 22 '19 at 02:36
  • @TitoPiezasIII yes, it can be done using the same method as in this MO post by Robert Bryant https://mathoverflow.net/a/197966/82588 – Martin Nicholson Jul 22 '19 at 08:57
  • @Nemo: If I may ask, can you edit your post and add the series form of the integral $(1)$? I'm not proficient with such transformations. – Tito Piezas III Jul 22 '19 at 11:00
  • @TitoPiezasIII the series is the same $$\ _4F_3(\frac{1}{2},1,1,2;\frac{5}{4},\frac{3}{2},\frac{7}{4};\frac{3}{4})$$ – Martin Nicholson Jul 22 '19 at 11:24
  • @Nemo: Oh. I thought it would be different. Thanks, anyway. – Tito Piezas III Jul 22 '19 at 11:26
  • Are both $(1)$ and $(2)$ equivalent to the conjectural identity of $L(2,\chi)$ at MO? – pisco May 07 '20 at 12:19
  • @pisco yes. $\phantom{}$ – Martin Nicholson May 07 '20 at 12:43
  • 1
    Not sure how much it can help, but after a few substitutions there is: $$\int_0^{{\pi }/{3}} P(x)\frac{xdx}{\sin x \sqrt{\frac{3}{4}-\sin ^2x}} = \sqrt[4]{3}\int_0^\infty \frac{\arcsin\left(\frac{\sqrt{3x}}{1+x}\right)}{\sqrt{1+x^3}}\frac{dx}{x}$$ – Zacky May 07 '20 at 21:54
  • 2
    @Nemo I recently posted an answer on MO, this settles your problem. Looking at your previous arXiv publications, you might be interested in other conjectures from arXiv:1010.4298 or arXiv:2210.07238. FYI, All infinite series conjectures in former article have been proved. – pisco Jan 08 '23 at 11:37
  • @pisco can you convert your comment into an answer so that we can close the question? – Martin Nicholson Feb 17 '24 at 11:54

0 Answers0