Question :
The coefficients a,b,c of the quadratic equation $ax^2+bx+c=0$ are determined by throwing a die three times and reading off the value shown on the uppermost face of each die. i.e, if you throw a 1, 5 and 3 respectively, the equation is $1x^2+5x+3=0$.
Find the probabilities that the quadratic equation you obtain :
- has real roots;
- has complex roots;
- has equal roots.
Thank you for your attention.
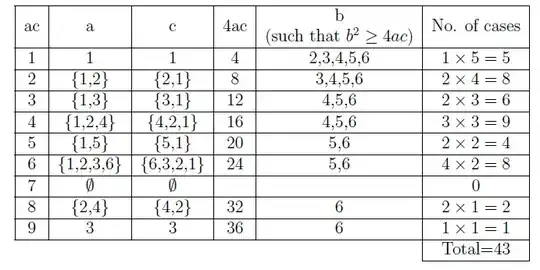
We show the path to the answers using somewhat tedious listing. The symmetry between $a$ and $c$ could be used to cut down on the work. We use the fact that the quadratic has real solutions if and only if the discriminant $b^2-4ac$ is $\ge 0$, and equal solutions if and only if $b^2-4ac=0$.
Equality is easiest. This happens if and only if $b^2=4ac$. That forces $b=2$, $4$, or $6$. If $b=2$, we need $a=c=1$, so the only configuration is $(1,2,1)$. If $b=4$, we want $ac=4$, which can happen in $3$ ways, $(1,4,4)$, $(4,4,1)$, and $(2,4,2)$. Finally, if $b=6$, we want $ac=9$, which only happens with the configuration $(3,6,3)$. Each configuration has probability $\frac{1}{6^3}$, so the required probability is $\frac{5}{216}$.
For real solutions , we want $b^2\ge 4ac$. That cannot happen if $b=1$. If $b=2$, it can only happen if $ac=1$, giving a contribution of $\frac{1}{216}$. If $b=3$, we want $ac\le 2$, which can happen in $3$ ways, for a contribution of $\frac{3}{216}$.
We leave the cases $b=4$ and $b=5$ to you. For $b=6$, we want $ac\le 9$. Let us list the ways. With $a=1$, $b$ can have $6$ values. With $a=2$ there are $4$. With $a=3$ there are $3$. With $a=4$ there are $2$. And there are $1$ each for $a=7$ and $a=6$. That gives a contribution of $\frac{17}{216}$.
For complex, one could say that the probability is $1$, since every real number is in particular a complex number. But what is probably intended is complex and non-real. Then the required probability is $1$ minus the probability the root(s) are real.
The roots of the above quadratic equation will be real if the discriminant will be non-negative, $ i.e. $ if $$b^2-4ac\geq 0 \Rightarrow b^2\geq 4ac $$
It is clear that $ a,b,c\in \{1,2,3,4,5,6\} $ as they are determined by throwing the dice.
$ \therefore\ $ the total number of possible outcomes is $ 6\times 6 \times 6=216. $
Let us find the total no. of favorable cases for the above-required probability:
Since, $ b^2\geq4ac $ and since the maximum value of $ b^2 $ is 36, $ ac=10,11,12,\ldots,36 $ is not possible. So, the probability that the above equation has real root is $ \frac{43}{216} $ $ \therefore $ Required probability $= 1-\frac{43}{216} =\frac{173}{216}$
Hint: Given the discrete random coefficients, $a, b, c \sim U(1, 6)$, the discriminant of the quadratic equation, $\displaystyle \Delta = b^2 -4ac$, determines whether or not you get real or complex values and whether or not they are distinct. If $\Delta > 0$ then x is a distinct real with two values., $\Delta = 0$, then x is real with one distinct value, otherwise x is complex with two distinct values.
Thus you are looking for $\mathbb{P}(\Delta < 0)$, $\mathbb{P}(\Delta = 0)$ and $\mathbb{P}(\Delta > 0)$. Which can be determined by the method of moment generating functions.
