Each coefficient in the equation $ ax^2 +bx+c = 0 $ is determined by throwing an ordinary die. Find the probability that the equation will have no real root. The only thing I know is $$a,b,c\in\{1,2,3,4,5,6\}$$
Asked
Active
Viewed 1,139 times
0
-
I am unable to start. – user360774 Aug 11 '16 at 17:24
-
Do you know the condition on $a,b,c$ to have non real roots? – Extremal Aug 11 '16 at 17:24
-
Yes the discriminant is less than 0. $b^2-4ac<0$ – user360774 Aug 11 '16 at 17:27
1 Answers
1
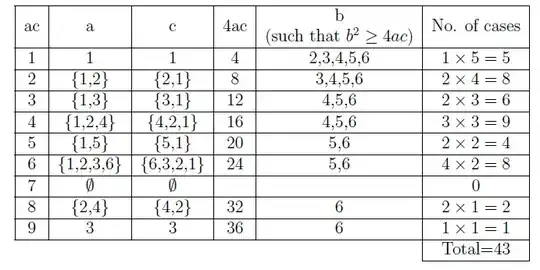
The roots of the above quadratic equation will be real if the discriminant will be non-negative, $ i.e. $ if $$b^2-4ac\geq 0 \Rightarrow b^2\geq 4ac $$
It is clear that $ a,b,c\in \{1,2,3,4,5,6\} $ as they are determined by throwing the dice.
$ \therefore\ $ the total number of possible outcomes is $ 6\times 6 \times 6=216. $
Let us find the total no. of favorable cases for the above-required probability:
Since, $ b^2\geq4ac $ and since the maximum value of $ b^2 $ is 36, $ ac=10,11,12,\ldots,36 $ is not possible. So, the probability that the above equation has real root is $ \frac{43}{216} $ $ \therefore $ Required probability $= 1-\frac{43}{216} =\frac{173}{216}$
Sachchidanand Prasad
- 2,770
-
-
1You are welcome. But it's my advice that you should try these questions on your own. Because these will give you more confidence for tougher problems. So try by yourself. Good luck! – Sachchidanand Prasad Aug 11 '16 at 17:38