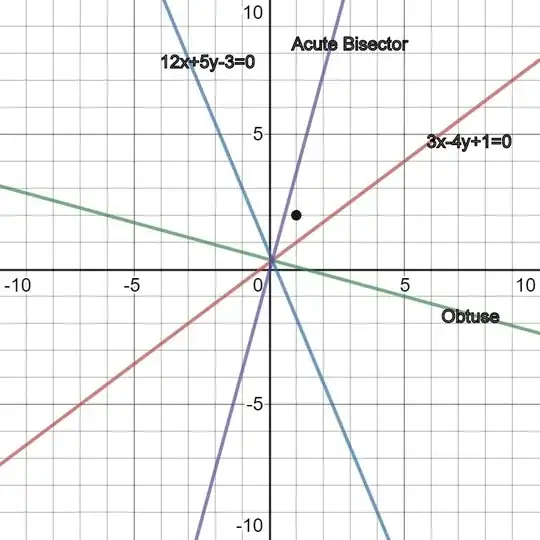
The geometric considerations in this proof of the bisector formula suggest a solution. Specifically, given a line $\lambda x+\mu y+\tau = 0$ and a point $(x_0,y_0)$, the sign of $\lambda x_0+\mu y_0+\tau$ allows us to identify the half-plane in which the point lies relative to the normal $(\lambda,\mu)$ to the line.
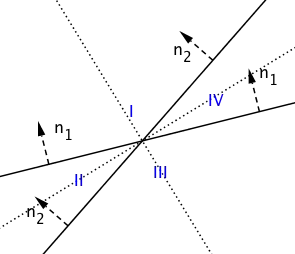
In the above diagram (reproduced from the referenced answer), we are given the lines $ax+by+c=0$ and $px+qy+r=0$, with respective normals $\mathbf n_1=(a,b)$ and $\mathbf n_2=(p,q)$. For a point $(x_0,y_0)$ in regions I and III, the signs of $ax+by+c$ and $px+qy+r$ are the same, whereas for points in regions II and IV they are different. That is, if the product of the signs of those two expressions is positive, the point is in an odd-numbered region and if it’s negative, the point is in an even-numbered region. The same pattern of signs applies to an arbitrary point $(x,y)$ on either bisector (other than the intersection of the given lines), leading to the identity $$\operatorname{sgn}(ax_0+by_0+c)\operatorname{sgn}(px_0+qy_0+r) = \operatorname{sgn}(ax+by+c)\operatorname{sgn}(px+qy+r).$$ Each of the terms in this identity is equal to $\pm1$, so this can be rearranged into $$\operatorname{sgn}(px_0+qy_0+r)\operatorname{sgn}(ax+by+c) = \operatorname{sgn}(ax_0+by_0+c)\operatorname{sgn}(px+qy+r).$$ Points on an angle bisector of two lines are distinguished by being at the same distance from each line, so we multiply both sides of the above identity by this distance and simplify to obtain
$$\operatorname{sgn}{(px_0+qy_0+r)}{ax+by+c\over\sqrt{a^2+b^2}} = \operatorname{sgn}(ax_0+by_0+c){px+qy+r\over\sqrt{p^2+q^2}}. \tag{*}$$
Applying this to the problem at hand, an equation of the bisector that passes through the same region as $(1,2)$ is $$\operatorname{sgn}(12\cdot1+5\cdot2-3){3x-4y+1\over 5} = \operatorname{sgn}(3\cdot1-4\cdot2+1){12x+5y-3\over13},$$ which can be simplified and rearranged into $99x-27y-2=0$.