Preliminaries (algorithm for solving a pair of quadratic equations of two variables):
It boils down to finding an algorithm for solving a system of two quadratic equations of two variables, by interpreting it as a projective geometry pencil of conics, then finding the three degenerate conics of the pencil together with a projective transformation that simplifies these three degenerate conics to the point of your being able to read off the solutions very easily in new simplifying coordinate system, and after that transforming them back to the original coordinate system.
I sketched an algorithm in python, I think it seems to work on your example... but I was in a hurry and did not check it properly, so there may be bugs...
import numpy as np
import math
technical module, functions, details
def homogenize(x):
return np.array([x[0], x[1], 1])
def cos_sin(angle_deg):
return math.cos(angle_degmath.pi/180), math.sin(angle_degmath.pi/180)
def rotation(cs_sn):
return np.array([[cs_sn[0], -cs_sn[1]],
[cs_sn[1], cs_sn[0]]])
defining the isometry (the rotation plus translation) transformation
between the coordinate system aligned with the conic and a general (world)
coordinate system
def isom_inverse(angle, translation):
'''
isometry from conic-aligned coordinate system (conic attached)
to global coordinate system (world system)
'''
cos_, sin_ = cos_sin(angle)
return np.array([[cos_, -sin_, translation[0]],
[sin_, cos_, translation[1]],
[ 0, 0, 1]])
def isom(angle, translation):
'''
isometry from global coordinate system (world system)
to conic-aligned coordinate system (conic attached)
'''
cos_, sin_ = cos_sin(-angle)
tr = - rotation((cos_, sin_)).dot(translation)
return np.array([[ cos_, -sin_, tr[0]],
[ sin_, cos_, tr[1]],
[ 0, 0, 1 ]])
calculating the coinc defined by a pair of axes' lengts,
axes rotation angle and center of the conic
def Conic(major, minor, angle, center):
D = np.array([[minor**2, 0, 0],
[ 0, major**2, 0],
[ 0, 0, -(minormajor)*2]])
U = isom(angle, center)
return (U.T).dot(D.dot(U))
calculating the coinc dual to the conic defined by a pair of axes' lengths,
axes rotation angle and center of the conic
def dual_Conic(major, minor, angle, center):
D_1 = np.array([[major**2, 0, 0],
[ 0, minor**2, 0],
[ 0, 0, -1]])
U_1 = isom_inverse(angle, center)
return (U_1).dot(D_1.dot(U_1.T))
transforming the matrix of a conic into a vector of six coefficients
of a quadratic equation with two variables
def conic_to_equation(C):
'''
c[0]x2 + c[1]xy + c[2]y*2 + c[3]x + c[4]y + c[5] = 0
'''
return np.array([C[0,0], 2C[0,1], C[1,1], 2C[0,2], 2C[1,2], C[2,2]])
transforming the vector of six coefficients
of a quadratic equation with two variables into a matrix of
the corresponding conic
def equation_to_conic(eq):
'''
eq[0]x2 + eq[1]xy + eq[2]y*2 + eq[3]x + eq[4]y + eq[5] = 0
'''
return np.array([[2eq[0], eq[1], eq[3]],
[ eq[1], 2eq[2], eq[4]],
[ eq[3], eq[4], 2eq[5]]]) / 2
given a point (x,y) define the vector (x^2, xy, y^2, x, y, 1)
def argument(x):
return np.array([x[0]2, x[0]*x[1], x[1]2, x[0], x[1], 1])
given x = (x[0],x[1]) calculate the value of the quadratic equation with
six coefficients coeff
def quadratic_equation(x, coeff):
'''
coeff[0]x2 + coeff[1]xy + coeff[2]y*2 + coeff[3]x + coeff[4]*y + coeff[5] = 0
'''
return coeff.dot( argument(x) )
given a pair of conics, as a pair of symmetric matrices,
calculate the vector k = (k[0], k[1], k[2]) of values for each of which
the conic c1 - k[i]c2 from the pencil of conics c1 - tc2
is a degenerate conic (the anti-symmetric product of a pair of linear forms)
and also find the matrix U
of the projective transformation that simplifies the geometry of
the pair of conics, the geometry of the pencil c1 - t*c2 in general,
as well as the geometry of the three degenerate conics in particular
def transform(c1, c2):
'''
c1 and c2 are 3 by 3 symmetric matrices of the two conics
'''
c21 = np.linalg.inv(c2).dot(c1)
k, U = np.linalg.eig(c21)
return k, U
the same as before, but for a pair of equations instead of matrices of conics
def eq_transform(eq1, eq2):
'''
eq1 and eq2 = np.array([eq[0], eq[1], eq[2], eq[3], eq[4], eq[5]])
'''
C1 = equation_to_conic(eq1)
C2 = equation_to_conic(eq2)
return transform(C1, C2)
realizing the matrix U as a projective transformation
def proj(U, x):
if len(x) == 2:
x = homogenize(x)
y = U.dot(x)
y = y / y[2]
return y[0:2]
find the common points, i.e. points of intersection of a pair of conics
represented by a pair of symmetric matrices
def find_common_points(c1, c2):
k, U = transform(c1, c2)
L1 = (U.T).dot((c1 - k[0]c2).dot(U))
L2 = (U.T).dot((c1 - k[1]c2).dot(U))
sol = np.empty((4,3), dtype=float)
for i in range(2):
for j in range(2):
sol[i+2*j,0:2] = np.array([math.sqrt(abs(L2[2,2] / L2[0,0]))(-1)i, math.sqrt(abs(L1[2,2] / L1[1,1]))(-1)*j])
sol[i+2j,0:2] = proj(U, sol[i+2*j,0:2])
sol[:,2] = np.ones(4)
return sol
find the solutions, i.e. the points x=(x[0],x[1]) saisfying the pair
of quadratic equations
represented by a pair of vectors eq1 and eq2 of 6 coefficients
def solve_eq(eq1, eq2):
conic1 = equation_to_conic(eq1)
conic2 = equation_to_conic(eq2)
return find_common_points(conic1, conic2)
'''
Esample of finding the common tangents of a pair of conics:
conic 1: major axis = 2, minor axis = 1, angle = 45, center = (0,0)
conic 2: major axis = 3, minor axis = 1, angle = 120, center = (15,0)
'''
a = 2
b = 1
cntr = np.array([0,0])
w = 45
Q1 = Conic(a, b, w, cntr)
dQ1 = dual_Conic(a, b, w, cntr)
a = 3
b = 1
cntr = np.array([15,0])
w = 120
Q2 = Conic(a, b, w, cntr)
dQ2 = dual_Conic(a, b, w, cntr)
R = find_common_points(dQ1, dQ2)
print('')
print(R)
print('')
print('checking that the output forms common tangent lines: ')
print('')
print('conic 1: ')
print(np.diagonal(R.dot(dQ1.dot(R.T))) )
print('')
print('conic 2: ')
print(np.diagonal(R.dot(dQ2.dot(R.T))) )
#conic_to_equation(dQ1)
Some Explanations: Assume you want to find the intersection points of two conics C1 and C2. Let us assume for simplicity that they are real ellipses that intersect in four different points (to avoid complex numbers)
In the case of finding the common tangents to a pair of conics,
simply convert the two conics two corresponding duals and then find the intersection points
of the duals. These intersection points are the equation coefficients of the tangents of the original conics.
There are possibly several different geometric interpretations of this problem, but let us go with the pencil of conics. The two conics C1 and C2 are represented by 3 by 3 symmetric matrices with non-zero determinants, which I have denoted C1 and C2. The linear combination, called pencil of conics generated by C1 and C2, is the t-parametrized family of conics C1 - t*C2 , where t is just a number. What is crucial is that every conic C1 - tC2 passes through the intersection points of C1 and C2 and these are the only four points they all have in common. You can prove this by observing that if x.T * C1 * x = x.T * C1 * x = 0 then
x.T * (C1 - t*C2) * x = x.T * C1 * x - t * x.T * C2 * x = 0 - t*0 = 0. Furthermore, if you take an intersection point of C1 and C1 - t*C2, then C2 = C1 - t*C2 + s*C2 you can apply the same argument when s = t.
In this family of conics, there are three degenerate conics, that are geometrically three pairs of lines. They occur exactly when t is such that det( C1 - t*C2 ) = 0. This is a polynomial equation of degree 3 with respect to t, so there are three, say different solutions k[0], k[1], k[2], due to the niceness of the C1 and C2. Projectively speaking, each degenerate conic C1 - k[j]*C2 is a pair of lines and they have a common intersection point u[:,j] = [ u[0,j] : u[1,j] : u[2,j] ]. Moreover, rank(C1 - k[j]*C2) = 2, so ker(C1 - k[j]*C2) = 1. This point u[:,j] is characterized as a solution to the equation
(C1 - k[j]*C2) * u[:,j] = 0.
Since C2 is invertible (non-degenerate), multiply both sides of the equation by inverse(C2) and obtain the equivalent equation ( (inverse(C2) * C1) - k[j]*Identity ) * u[:,j] = 0 which is an eigenvalue equation, with k[j] as eigenvalue and u[:,j] as eigenvector. The output of the function transform() is the 1 by 3 array k of eigenvalues and the 3 by 3 matrix U = [ u[:,0], u[:,1], u[:,2] ] of eigenvectors.
Conjugating C1 - k[j]*C2 by U, i.e. (U.T)*(C1 - k[j]*C2)*U, is geometrically equivalent to performing a projective transformation that sends u[:,0] and u[:,1] to infinity and u[:,2] to the origin. Thus, U changes the coordinate system from a general one to a special coordinate system, in which two of the degenerate conics are given by pairs of parallel lines and combined they intersect in a rectangle. The third conic is represeneted by the diagnols of the rectangle.
In this new picture, the intersection problem can be easily solved, just by reading off one solution from the entries of the matrices (U.T)*(C1 - k[j]*C2)*U (the intersection points are the vertices of the rectangle, so if you find one of them, the others are simply mirror symmetric of each other).
Some explanations on how the solutions in special coordinates are obtained.
Since, by construction (by the special choice of eigenvalues k[0] and k[1]) the original conics C1 - k[0]*C2 and C1 - k[1]*C2 are degenerate and thus a pair of lines each, after the projective transformation U, which simplifies the conics and represents them by the matrices L1 = (U.T)*(C1 - k[0]*C2)*U and L1 = (U.T)*(C1 - k[0]*C2)*U, are diagonal and thus geometrically each of these is a pair of lines, parallel one of the coordinate axes, e.g. L1 is a pair of lines parallel to x and L2 is a pair of lines parallel to y. Also for each degenerate conic, the pair of lines are symmetric with respect to the coordinate axes. Hence, the four intersection points form the vertices of a rectangle, mirror symmetric relative to the coordinate axes. Thus, the intersection points are of the projective form
sol[0, : ] = [ sol[0, 0], sol[0, 1], 1]
sol[1, : ] = [-sol[0, 0], sol[0, 1], 1]
sol[2, : ] = [-sol[0, 0], -sol[0, 1], 1]
sol[3, : ] = [ sol[0, 0], -sol[0, 1], 1]
so it is enough to find only one of them and then reflect it across the coordinate axes. In the simplifying coordinate system, the conic L1 has the an equation like this
(a1*y - b1) * (a1*y + b1) = 0
where the two lines are a1*y = b1 and a1*y = -b1 so the y coordinate of one of the solutions should be y = abs(b1/a1). If you expand the equation, you get the quadratic equation
a1^2 * y^2 - b1^2 = 0
and in matrix form
0 0 0
L1 = 0 L1[1,1] 0
0 0 L1[2,2]
where L1[1,1] = a1^2 and L1[2,2] = b1^2
Hence, the y coordinate of one solution is
y = abs(b1/a1) = sqrt( abs( L1[2, 2] / L1[1, 1] ) )
If you do the same for the conic L2, but this time thinking about it being a pair of symmetric lines parallel to the y axis, then you get the x coordinate of a solution
x = abs(b2/a2) = sqrt( abs( L2[2, 2] / L2[1, 1] ) )
That is why, one solution is
sol[0, :] = [ sqrt(abs( L2[2, 2] / L2[1, 1] )), sqrt(abs( L1[2, 2] / L1[1, 1] )), 1]
Then all solutions are obtained by reflecting in the coordinate axes:
sol[, :] = [(-1)**i*sqrt(abs( L2[2, 2] / L2[1, 1] )), (-1)**j*sqrt(abs( L1[2, 2] / L1[1, 1] )), 1]
for i = 0,1 and j=0,1
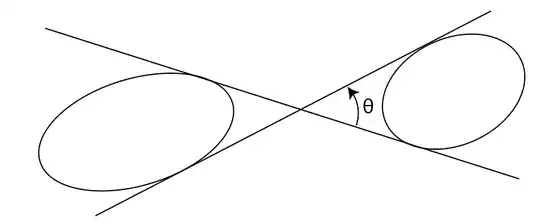
Algorithm for calculating the angle between the internal tangents:
import numpy as np
import math
'''
####### FUNCTIONS IMPORTANT FOR THE CALCULATION #######
'''
def homogenize(x):
return np.array([x[0], x[1], 1])
transforming the vector of six coefficients
of a quadratic equation with two variables into a matrix of
the corresponding conic
def conic_from_equation(eq):
'''
eq is an np.array vector of the equadratic equation's six coefficients
eq[0]x2 + eq[1]xy + eq[2]y*2 + eq[3]x + eq[4]y + eq[5] = 0
conc is a symmetric matrix of the bilinier form of the quadratic equation
'''
return np.array([[2eq[0], eq[1], eq[3]],
[ eq[1], 2eq[2], eq[4]],
[ eq[3], eq[4], 2eq[5]]]) / 2
obtaining the conic dual to a given conic,
both represented as symmetric 3x3 matrices
def dual_conic(conic):
return np.linalg.inv(conic)
given a pair of conics, as a pair of symmetric 3x3 matrices,
calculate the vector k = (k[0], k[1], k[2]) of values for each of which
the conic c1 - k[i]c2 from the pencil of conics c1 - tc2
is a degenerate conic (the anti-symmetric product of a pair of linear forms)
and also find the matrix U
of the projective transformation that simplifies the geometry of
the pair of conics, the geometry of the pencil c1 - t*c2 in general,
as well as the geometry of the three degenerate conics in particular
def trivialization_of(conic1, conic2):
'''
c1 and c2 are 3 by 3 symmetric matrices of two conics (possibly dual)
'''
c21 = np.linalg.inv(conic2).dot(conic1)
k, U = np.linalg.eig(c21)
return k, U
realze the 3x3 matrix U as a projective transformation of projective 2-plane
def projectivity(U, x):
if len(x) == 2:
x = homogenize(x)
y = U.dot(x)
y = y / y[2]
return y[0:2]
find the common points, i.e. points of intersection of a pair of conics
represented by a pair of symmetric matrices
def find_intersection_points(c1, c2):
k, U = trivialization_of(c1, c2)
L1 = (U.T).dot((c1 - k[0]c2).dot(U))
L2 = (U.T).dot((c1 - k[1]c2).dot(U))
sol = np.empty((4,3), dtype=float)
for i in range(2):
for j in range(2):
sol[i+2*j,0:2] = np.array([math.sqrt(abs(L2[2,2] / L2[0,0]))(-1)i, math.sqrt(abs(L1[2,2] / L1[1,1]))(-1)*j])
sol[i+2j,0:2] = projectivity(U, sol[i+2*j,0:2])
sol[:,2] = np.ones(4)
return sol
find the three coefficients of all four common tangents to a pair of conics
make sure that the conics do have four common tangents,
which is the generic situation
def find_common_tangents(c1, c2):
dc1 = dual_conic(c1)
dc2 = dual_conic(c2)
return find_intersection_points(dc1, dc2)
if the two conics are ellipses, they do not intersect the line at infinity.
by polarity, the poles of the line at infinity are
the (affine and in fact metric) centers of the ellipses and are located
inside the ellipses each. We use them to detect the inner tangents and
to orient the vectors normal to these tangents in a way
so that the angle between these two normal vectors is the vector on the picture
def dual_to_infinity_line(conic):
p = dual_conic(conic).dot(np.array([0,0,1]))
return homogenize( p[0:2] / p[2] )
find the common inner tangents between a pair of conics,
represented as 3x3 symmetric matrices, with properly oriented normal vectors
def find_common_inner_tangents(c1, c2):
p1 = dual_to_infinity_line(c1)
p2 = dual_to_infinity_line(c2)
tn = find_common_tangents(c1, c2)
# boolean vector, true if inner tangent false if not
is_inner_tangent = ( tn.dot(p1)tn.dot(p2) < 0 )
tn = tn[ is_inner_tangent, : ]
# reorient one of the normal vectors so that they give us the proper angle
if tn[0,:].dot(p1)tn[1,:].dot(p1) > 0:
tn[1,:] = - tn[1,:]
return tn
calculate the angle between a pair of line, given by their three coefficients
def angle_bn_lines(line1, line2):
theta = line1[0:2].dot(line2[0:2]) / math.sqrt( line1[0:2].dot(line1[0:2])line2[0:2].dot(line2[0:2]))
return math.acos(theta)180/math.pi
calculate the proper angle between the inner tangents of two quadratic equations
that represent a pair of conics, hopefully non-intersecting
def angle_bn_inner_tangents_of(eq_of_conic1, eq_of_conic2):
c1 = conic_from_equation(eq_of_conic1)
c2 = conic_from_equation(eq_of_conic2)
tn = find_common_inner_tangents(c1, c2)
return angle_bn_lines(tn[0,:], tn[1,:])
'''
####### END OF FUCTIONS IMPORTANT FOR THE CALCULATION #######
'''
'''
####### auxiliary functions to handle the test scenario:
'''
def cos_sin(angle_deg):
return math.cos(angle_degmath.pi/180), math.sin(angle_degmath.pi/180)
def rotation(cs_sn):
return np.array([[cs_sn[0], -cs_sn[1]],
[cs_sn[1], cs_sn[0]]])
def isom(angle, translation):
'''
isometry from global coordinate system (world system)
to conic-aligned coordinate system (conic attached)
'''
cos_, sin_ = cos_sin(-angle)
tr = - rotation((cos_, sin_)).dot(translation)
return np.array([[ cos_, -sin_, tr[0]],
[ sin_, cos_, tr[1]],
[ 0, 0, 1 ]])
calculating the conic defined by a pair of axes' lengths,
axes rotation angle and center of the conic
def Conic(major, minor, angle, center):
D = np.array([[minor**2, 0, 0],
[ 0, major**2, 0],
[ 0, 0, -(minormajor)*2]])
U = isom(angle, center)
return (U.T).dot(D.dot(U))
transfromaing the matrix of a conic into a vector of six coeficients
of a quadratic equation with two variables
def equation_from_conic(C):
'''
c[0]x2 + c[1]xy + c[2]y*2 + c[3]x + c[4]y + c[5] = 0
'''
return np.array([C[0,0], 2C[0,1], C[1,1], 2C[0,2], 2C[1,2], C[2,2]])
'''
####### end of auxiliary functions
'''
'''
Example of finding the angle between the common tangents of a pair of conics:
conic 1: major axis = 2, minor axis = 1, angle = 45, center = (0,0)
conic 2: major axis = 3, minor axis = 1, angle = 120, center = (15,0)
'''
a = 2
b = 1
cntr = np.array([0,0])
w = 45
Eq1 = equation_from_conic(Conic(a, b, w, cntr))
Co1 = conic_from_equation(Eq1)
a = 3
b = 1
cntr = np.array([15,0])
w = 120
Eq2 = equation_from_conic(Conic(a, b, w, cntr))
Co2 = conic_from_equation(Eq2)
four_tngs = find_common_tangents(Co1, Co2)
inner_tngs = find_common_inner_tangents(Co1, Co2)
print( angle_bn_inner_tangents_of(Eq1, Eq2) )
Calculating the angle bisector line
of the inner tangents.
Here is a routine that, given a pair of lines line1 and line2, represented by vectors with three coefficients, calculates the three coefficients of the angle bisector line that splits the angle in half. It also returns the slope of the tangent line, as the ratio of the y-increase divided by the x-increase.
def angle_bisector(line1, line2):
n1 = line1[0:2]
n2 = line2[0:2]
n1 = n1 / math.sqrt(n1.dot(n1))
n2 = n2 / math.sqrt(n2.dot(n2))
n_bsec = n1 + n2
p12 = np.cross(line1, line2)
p12 = p12[0:2] / p12[2]
c_bsec = n_bsec.dot(p12)
return np.array([n_bsec[0], n_bsec[1], c_bsec]), np.array([-n_bsec[1], n_bsec[0]])
def angle_and_bsec_vector_bn_inner_tangents_of(eq_of_conic1, eq_of_conic2):
c1 = conic_from_equation(eq_of_conic1)
c2 = conic_from_equation(eq_of_conic2)
tn = find_common_inner_tangents(c1, c2)
if abs(np.all(tn.imag)) < 1e-10:
tn = tn.real
p1 = dual_to_infinity_line(c1)[0:2]
p2 = dual_to_infinity_line(c2)[0:2]
bsec, v_bsec = angle_bisector(tn[0], tn[1])
angle = angle_bn_C_lines(tn[0,:], tn[1,:])
if abs(angle.imag) < 1e-10:
angle = angle.real
if v_bsec.dot(p2 - p1) < 0:
v_bsec = - v_bsec
return angle, v_bsec / np.linalg.norm(v_bsec)