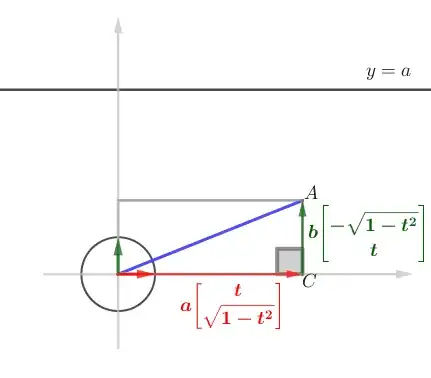
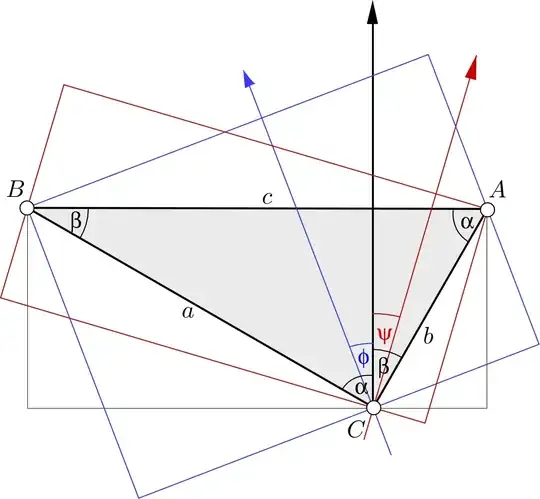
Geometric argument
Let's start with a geometric approach that reverses the roles of the square and the triangle, fixing a (say) unit square and finding the largest right triangle with sides in proportion to 5:12:13 that can fit within.
Clearly the largest such triangle would touch the square's perimeter, since otherwise the triangle can be uniformly enlarged. Indeed there must be at least two vertices in contact, since if there were only one vertex on the perimeter, we could expand the triangle from that vertex.
For some triangle shapes placing just two vertices in contact with the perimeter gives the largest triangle, namely for those shapes where the longest side can be placed along a diagonal of the square and the third vertex falls inside one or the other half of the square. A picture of a semicircle drawn on the diagonal of the square should convince us that among right triangles, only the isosceles right triangle can be be so positioned. Thus the 5:12:13 triangle will not fit in that way.
Building on this, we claim (A) that the largest triangle with this 5:12:13 shape will have all three vertices on the square's perimeter and (B) that such a triangle will touch all four sides of the square. We will briefly sketch arguments for both claims, motivated by noting that from these it follows one of the triangle's vertices must touch upon two sides of the square, i.e. at a corner of the square.
Claim A: The cases of zero or one vertex being on the square's perimeter have already been sufficiently described. Suppose exactly two vertices are on that perimeter, e.g. the endpoints of one edge of the triangle. Here are the possible cases:
Both endpoints on a common edge of the square. If not the entire edge, then the triangle can be enlarged to cover more of it or cause the third vertex to touch the square's perimeter. If it is then entire edge, the triangle can be rotated about one of these endpoints (having an acute angle), lifting the other endpoint off the perimeter.
The two endpoints are incident to adjacent edges of the square (but not as in case 1). Except when this edge coincides with the square's diagonal (previously ruled out), the triangle can again be rotated about one of these endpoints to lift the other endpoint off the perimeter.
The two endpoints are incident to opposing edges of the square (but not as in case 2). The triangle can be rotated about the midpoint of that edge (since neither is in a corner of the square). lifting both away from the perimeter.
Of course once the number of vertices on the perimeter is reduced, the triangle can be enlarged until vertices again meet the perimeter. The largest possible 5:12:13 triangle will thus have all three vertices on the square's perimeter.
Claim B: We sketch an argument valid for all right triangles, noting that it falls short when applied to (strictly) acute triangles. Suppose a 5:12:13 (right) triangle has all three vertices on the perimeter of the square. In order to enlarge it (without touching all four sides), we intend to rotate the triangle so that one vertex moves inside the square, after which claim A can be applied.
If the triangle does not touch a pair of opposing sides, i.e. it touches at most a pair of adjacent sides of the square, then we can already enlarge it until an opposing side is reached. So without loss of generality we may assume the triangle touches all but one of the four sides of the square. To make a mental image, assume it is the top edge of the square untouched by the triangle.
We've already mentioned that the isoceles right triangle can be maximized by aligning it with the square's diagonal, and of course in this position it touches all four edges. Now assuming we have another kind of right triangle, it must be a scalene triangle (all sides are different lengths). For convenience we can refer to the short leg, the longer leg, and the (longest) hypotenuse.
The possibilities can be classified by asking where the right angle of the triangle touches the square. (1) It might be in a corner of the square (bottom edge), so that the longer leg is actually shared with the square's bottom edge. (2) It might be in the interior of the square's bottom edge. (3) It might be on the left or right edge of the square (but not in the corner).
In case (1) the triangle can be rotated "up" from the bottom edge around the vertex where the shorter leg and hypotenuse of the triangle meet.
In case (2) the triangle can be rotated "up" from the bottom edge around whichever vertex on the left or right edge is lower (either of them if they are at the same height).
In case (3) the triangle can be rotated "up" around the right angle vertex (whether it touches the left or the right side of the square).
Some pictures will of course be helpful here to supplement the mental image, and I will try to find time to post them.
Now, as previously remarked, the claims A and B suffice to force one of the vertices of the triangle to coincide with a corner of the square (because we have the three triangle vertices touching the four edges of the square). A little thought shows further that this can only be accomplished if the vertex of the triangle with the smallest angle (opposite the shortest leg) is the one incident with a corner of the square.
With that observation we are nearly finished determining the largest (similar) 5:12:13 right triangle that can be fitted into (say) a unit square. Indeed the Question itself presents an image of that arrangement. Instead of providing the calculations here, I will instead provide a more rigorous computation involving the so-called rotating calipers approach.
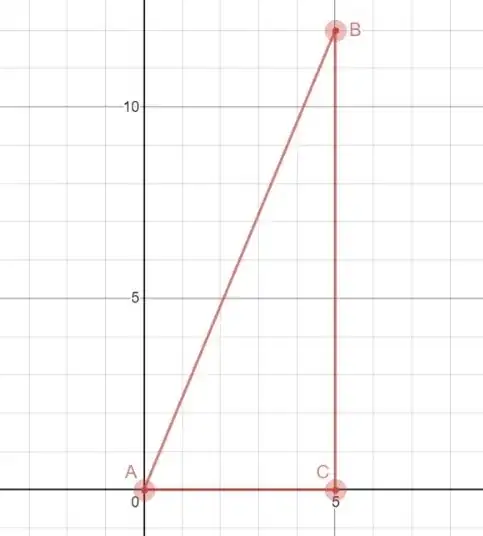
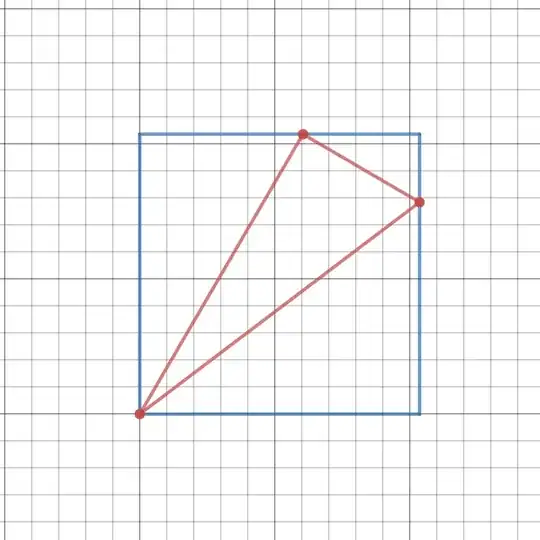 It is the smallest because whatever it is rotated clockwise/anti-clockwise through the origin, the side length of square will be larger.
It is the smallest because whatever it is rotated clockwise/anti-clockwise through the origin, the side length of square will be larger.