I hope it's valid to ask for "a more neat solution" of a problem on this network, despite the fact that I don't have a strict definition of the word "neat".
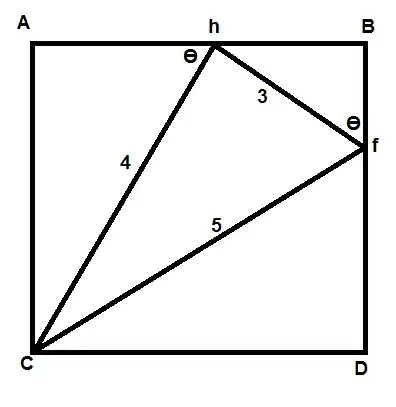
Here is the square and the right triangle inscribed in it.
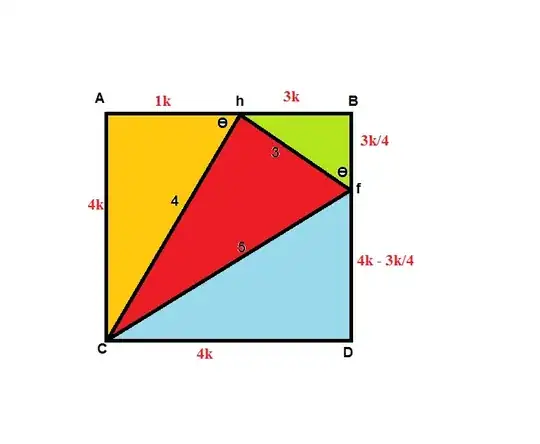
I did the following: $$AC = Ah + hB$$ $$4\sin\theta = 4\cos\theta + 3\sin\theta$$ So $$\tan\theta = 4$$ But $$\sin\theta = \frac{\tan\theta}{\sqrt{1+\tan^2\theta}}$$ Therefore $$AC = 4\sin\theta = \frac{16}{\sqrt {17}}$$ $$\text{Area} = \left(\frac{16}{\sqrt {17}}\right)^2$$
Without using trigonometry:
enjoy...
By coloring triangles the same I am trying to emphasize the similar triangles, which are not necessarily equal (although red and blue triangles are). I don't mean that the triangles with the same color has the same area, be careful.
I think your way is good, but we don't need to find $\tan\theta$.
From $4\sin\theta=4\cos\theta+3\sin\theta$, we have $$\sin\theta=4\cos\theta$$ Squaring the both sides gives $$\sin^2\theta=16(1-\sin^2\theta)$$ from which we can have $$\sin^2\theta=\frac{16}{17}\quad\Rightarrow\quad \text{(area)}=16\sin^2\theta=\frac{16^2}{17}$$
Here it's another way. The triangles AhC and Bhf are similar. If you put $Bh=x$ and $Bf=y$ you get the relations $$x+\frac{4}{3}y=\frac{4} {3} x$$ $$9=x^2+y^2$$ From which you can obtain the length of the side and then the area
Here is another way of doing it.
After discovering that $\tan \theta = 4$, all the line segments can then be expressed in terms of k with Ah = 1k as a start.
Find the value of $k^2$ from $$16k^2 – \triangle yellow – \triangle green – \triangle blue = \triangle red = \dfrac {3 \times 4}{2}$$
Required area follows.
I wanted to make this a comment but my reputation is not high enough. I believe your way is the best and it's actually rather clever. Your formula has a typo (forgot to square the tangent in the denominator. $$\sin(\theta)=\frac{\tan(\theta)}{\sqrt{1+\tan^2(\theta)}}$$
This formula is easily derived by considering a right triangle with legs $\tan(\theta)$ and $1$ (and therefore hypotenuse $\sqrt{1+\tan^2(\theta)}$. That will be true for all right triangles by the definition of tangent.
Denote: $AB=a, BF=x, BH=y$. Then: $$\begin{cases}a^2+(a-x)^2=25 \ (1)\\ (a-y)^2+a^2=16 \ (2)\\ x^2+y^2=9 \ (3)\end{cases}$$ $(1)-(2)$: $$(a-x)^2-(a-y)^2=x^2+y^2 \Rightarrow 2a(y-x)=2y^2 \Rightarrow a=\frac{y^2}{y-x} \ \ \ \ \ \ \ \ \ \ \ (4)$$ $(4)\to (2)$: $$\begin{align}\left(\frac{y^2}{y-x}-y\right)^2+\left(\frac{y^2}{y-x}\right)^2&=16 \Rightarrow \\ \frac{y^2(x^2+y^2)}{(y-x)^2}&=16 \stackrel{(3)}\Rightarrow \\ 9y^2&=16(9-2xy) \stackrel{(3)}\Rightarrow \\ 144-9y^2&=32y\sqrt{9-y^2} \Rightarrow \\ 1104y^4-11808y^2+20736&=0 \Rightarrow \\ y_1&=\frac{12}{\sqrt{17}}; y_2=\frac{12}{\sqrt{65}} \Rightarrow \\ x_1&=\frac3{\sqrt{17}}; x_2=\frac{21}{\sqrt{65}}.\end{align}$$ Hence, from $(4)$: $$a=\frac{y^2}{y-x}=\frac{\frac{144}{17}}{\frac9{\sqrt{17}}}=\frac{16}{\sqrt{17}}\\ y-x<0 \Rightarrow a\in \emptyset$$ Reference: WA answer.
Noting CAh and hBf are similar triangles in the linear ratio 4:3, redraw the original figure in a 4x4 square. The square of its hypotenuse Ch² is therefore 17 (see figure) - which is too large, it should be 4² or 16. Since the area of any similar figure is proportional to the square of any of its linear dimensions, simply scale the 4x4 square by 16/17 to find the area of the original figure: 16²/17
let's say $AC=x$ , $Ah=y$ and therefore $hB=x-y$. $hAC$ and $fBh$ are similar triangles so:
$\frac{x}{4}=\frac{x-y}{3} $
$y=\frac{x}{4}$
$\frac{x^2}{16}+x^2=16$
$x^2=\frac{256}{17}$
