5

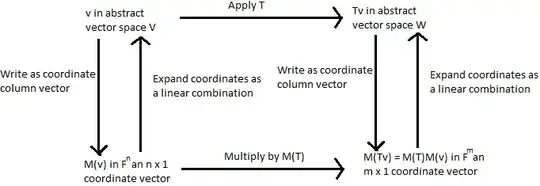
In Linear Algebra Done Right, it said

Suppose $T \in \mathcal{L}(V,W)$ and $v \in V$. Suppose $v_1,...,v_n$ is a basis of $V$ and $w_1,...,w_m$ is a basis of $W$. Then $$M(Tv) = M(T)M(v)$$

$M(T)$ is the m-by-n matrix whose entries $A_{j,k}$ are defined by $Tv_k = A_{1,k}w_1 + ... + A_{m,k}w_m$ suppose $T \in \mathcal{L}(V,W)$ and $v_1,...,v_n$ is a basis of $V$ and $w_1,...,w_m$ is a basis of $W$.

$M(v)$ is the matrix of vector $v$.

I generally follow the following proof:

Suppose $v = c_1v_1 + ... + c_nv_n$, where $c_1,...,c_n \in \mathbb{F}$. Thus $$Tv = c_1Tv_1 +...+c_nTv_n$$

Hence

\begin{equation} \begin{split} M(Tv) &= c_1M(Tv_1) + ...+ c_nM(Tv_n)\\ & = c_1M(T)_{.,1} +...+c_nM(T)_{.,n} \\ & = M(T)M(v) \end{split} \end{equation}

But I have questions on the meaning of the proof. The book said it means each m-by-n matrix $A$ induces a linear map from $\mathbb{F}^{n,1}$ to $\mathbb{F}^{m,1}$. The result can be used to think of every linear map as a matrix multiplication map after suitable relabeling via the isomorphisms given by $M$.

  1. Is the shape of $M(Tv)$ m by 1, $M(T)$ m by n, and $M(v)$ n by 1?
  2. What is meant by suitable relabeling via the isomorphisms given by $M$? Does it just mean $M(T)$ is a isomorphism linear map between $M(v)$ and $M(Tv)$?
Rodrigo de Azevedo
  • 1
JOHN
  • 1,176
  • 9
  • 26
  • In your blockquote, you haven't told us what $M$ means. – Gerry Myerson Apr 07 '19 at 07:02
  • @GerryMyerson revised – JOHN Apr 07 '19 at 07:13
  • Sorry, I don't know what it means for $M(v)$ to be the matrix of the vector $v$. What's the matrix of the vector $(1,2,3)$? – Gerry Myerson Apr 07 '19 at 07:15
  • 1
    @GerryMyerson Knowing Axler, it will be the coordinate vector for the given basis (in this case, $v_1, \ldots, v_n$). For example, if the basis is $(0, 0, 1), (0, 1, 1), (1, 1, 1)$ in the space $\Bbb{R}^3$, then $M(1, 2, 3) = \begin{bmatrix} 1 \ 1 \ 1 \end{bmatrix}$. – Theo Bendit Apr 07 '19 at 07:17

2 Answers2

21

In answer to your first question, yes to all three: $v$ is an element of the $n$-dimensional space $V$, so the coordinate vector with respect to the basis will be an $n \times 1$ column vector. Similarly, $Tv \in W$, which is an $n$-dimensional space, so $M(Tv)$ will be an $m \times 1$ column vector. Finally, $M(T)$ is built from transforming the $n$ basis vectors of the domain, forming each an $m \times 1$ coordinate column vector, which are put into an $m \times n$ matrix.

In answer to your second question, consult the following commutative diagram (made in Paint :( ):

enter image description here

The process of applying $T$ to a vector $v \in V$ is the top row of the diagram. However, there's a parallel process happening between $\Bbb{F}^n$ and $\Bbb{F}^m$, mirroring the same process.

The isomorphism being referred to are the double arrows, taking us between $V$ and $\Bbb{F}^n$ and $W$ and $\Bbb{F}^m$, by way of coordinate vectors. The coordinate vector map on $V$ is a linear map between $V$ and $\Bbb{F}^n$ that is invertible, making it an isomorphism (and similarly for $W$). That is, the two spaces are structurally identical, and anything we can do with one space, we can view it in the other.

In $V$, we have some abstract vectors, and an abstract linear transformation $T$ that maps vectors in $V$ to vectors in $W$. However, using this isomorphism, we can view $V$ slightly differently as $\Bbb{F}^n$, and similarly for $W$, which means $T$ boils down to a linear map from $\Bbb{F}^n$ to $\Bbb{F}^m$, which can be characterised as matrix multiplication. The matrix, in particular, is $M(T)$.

Theo Bendit
  • 50,900
  • Very nice graph! – JOHN Apr 07 '19 at 09:35
  • 5
    Upvote for the commutative paint diagram! – Jannik Pitt Apr 07 '19 at 13:27
  • it seems that T and M(T) is also isomorphic ? – JOHN Apr 07 '19 at 22:32
  • 1
    Isomorphisms are maps between vector spaces; only vector spaces can be isomorphic (at least, until you study category theory). The map $M$ (given fixed bases) is itself an isomorphism between the space of linear maps from $V$ to $W$ and the $m \times n$ matrices, but even then, it's not really correct to say that a map $T$ is "isomorphic" to a matrix $M(T)$. It would be more accurate (though not conventional) to describe the map $T$ as "similar" to the matrix $M(T)$, in a similar sense to similar matrices (bear in mind, $T$ is not a matrix). – Theo Bendit Apr 07 '19 at 23:02
  • 2
    @JOHN Simply put, vectors cannot be isomorphic. Maps cannot be isomorphic. Only spaces can be isomorphic. – Theo Bendit Apr 07 '19 at 23:06
4

  1. Yes, those would be the shapes of those vectors when represented as matrices. Given that we're multiply by vectors on the right.

  2. There is a theorem that if $V$ is an $n-$dimensional vector space over a field $F,$ then $V$ is isomorphic to $F^n.$ Here the isomorphic mappings assign coordinates to our vectors and our linear transformation. It doesn't mean that $M$ is an isomorphism between $M(v)$ and $M(Tv).$ These are particular vectors. The map $M$ actually induces an isomorphism from $V\to F^n$, isomorphism from $T\to F^{n\times m}$, and an isomorphism from $W\to F^m.$

I actually like the way that this is done. The Author is telling you that you're representation of $T$ by a matrix depends on your choice of basis in $F^n$. A fact that is important to remember.

Melody
  • 2,793