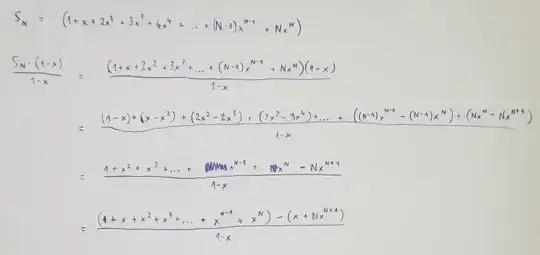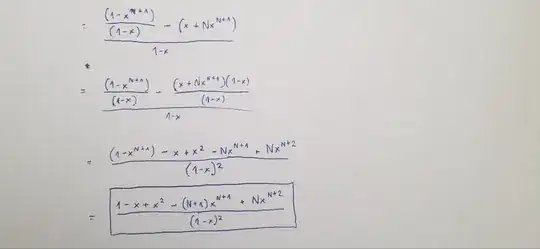How is the partial sum of a geometric sequence calculated?

Question

I have been asked to calculate a general formula for $1 + b + 2b^2 + 3b^3 + ... + Nb^N$

I think that a part of this is a geometric sequence, and I have rewritten this as

$f(x) = 1 + \sum_{i=1}^n i\cdot x^i$

(I couldn't figure out a way to make the first term be 1 with the progression so I just removed it from the series instead)

When I look on Wolfram Alpha it says that the partial sum formula for $ \sum_{i=1}^n i\cdot x^i$ is:

$$\sum_{i=1}^n i\cdot x^i = \frac{(nx-n-1)x^{n+1}+x}{(1-x)^2}$$

On this question, an answer said that the general formula for the sum of a finite geometric series is:

$$\sum_{k=0}^{n-1}x^k = \frac{1-x^n}{1-x}$$

But if I substitute my ($i\cdot x^i$) into the formula mentioned above I don't get the same value as the one Wolfram gives me.

Two questions:

1. Is it correct to pull the first term out of the series so it becomes a geometric series, or is there another way?
2. How did Wolfram Alpha calculate that expression?

Answer 1

The extra factor of $i$ or $k$ or whatever you call it means we no longer have a geometric series, but we can get one by differentiating with respect to $x$. You'll want to check powers of $x$ carefully too.

Answer 2

Hint: Think derivatives w.r.t. $b\,$:

$$1 + b + 2b^2 + 3b^3 + \dotsm + Nb^N=b\sum_{k=1}^{N}k\,b^{k-1}=b\Bigl(\sum_{k=0}^{N}b^k\Bigr)^{\!\!'}$$

Answer 3

Your presumptions are wrong. The first series is not a geometric series. and substituting $i*x^i$ into $\sum_{k=0}^N x^k$ is not the same as $\sum_{i=0}^Ni*x^i$.

Try to solve the problem using the principle of induction:

Let us assume the above relation holds for $n$: $\sum_{i=0}^n ix^i=\frac{(nx-n-1)x^{n+1}+x}{(1-x)^2}\equiv=A_n$.

Now let us show it must also holds for $n+1$ and therefore for all $n\in\mathcal{N}$. Thus,

\begin{align} \sum_{i=0}^{n+1}ix^i&=\underbrace{\sum_{i=0}^{n}ix^i}_{=A_n}+(n+1)x^{n+1}\\ &=A_n+(n+1)x^{n+1}\\ &=\frac{(nx-n-1)x^{n+1}+x}{(1-x)^2}+(n+1)x^{n+1}\\ &=\frac{(nx-n-1)x^{n+1}+x}{(1-x)^2}+(n+1)x^{n+1}\frac{(1-x)^2}{(1-x)^2}\\ &=\frac{(nx-n-1)x^{n+1}+x+(n+1)x^{n+1}*(x-1)^2}{(1-x)^2}\\ &=\frac{1}{(1-x)^2}\biggl((nx-n-1)x^{n+1}+x+(n+1)x^{n+1}(1+x^2-2x)\biggr)\\ &=\frac{1}{(1-x)^2}\biggl(x^{n+2}((n+1)x-n-2)+x\biggr)\\ &=\frac{1}{(1-x)^2}\biggl(x^{(n+1)+1}((n+1)x-(n+1)-1)+x\biggr) \end{align}

So if it holds for any $n$ it must hold for $n+1$ too and therefore for all natural numbers. Now, you only have to check that it holds for $n=0$ or $n=1$ and you are done.

Answer 4

Start with $$S=1 + b + 2b^2 + 3b^3 + \cdots + Nb^N$$

Multiply by $b$ and then subtract to give $$bS=b + b^2 + 2b^3 + 3b^4 + \cdots +(N-1)b^N + Nb^{N+1}$$ $$(b-1)S = -1 - b^2 - b^3 - b^4 - \cdots -b^N + Nb^{N+1}$$

Do that again $$b(b-1)S = -b - b^3 - b^4 - b^5 - \cdots -b^N-b^{N+1} - Nb^{N+2}$$ $$(b-1)^2S = 1-b +b^2 -(N+1)b^{N+1} + Nb^{N+2}$$

Finally simplify $$S = \dfrac{1-b +b^2 -(N+1)b^{N+1} + Nb^{N+2}}{(b-1)^2}.$$

As an example, with $b=2$ and $N=3$ the first line gives $S=1+2+8+24=35$ while the final line gives $S=\frac{1-2+4-64+96}{1^2}= 35$

Answer 5

Here's what I did to get the formula for partial sums of this series:

It was too much to type in LaTeX, so just did it on paper. Hope you don't mind.