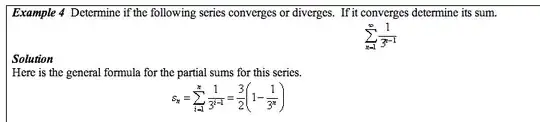3

im having trouble figuring out how to find the general formula for partial sums of a series.

Is it a trial and error kind of thing where I just have to figure it out?

or is there a systematic way to figure it out?

enter image description here

in that example from pauls calculus, I dont see how he got that general formula for the partial sums.

Thanks for the help.

user71317
  • 545
  • In certain cases, like yours, there is presented a general formula in DLMF 16.2.4 that will take a Generalized Hypergeometric function and sum the first n terms into another Generalized Hypergeometric function. Of course, the only advantage is, embedding the problem into an expression set that is analytic and a lot is known about. For instance, your expression, before summation/termination, would be 1F0(1;;1/3) and for an exponential finite summation 0F0(;a*t). It is a general statement embedded in "polynomials". I would have to check on the generality of it. Thought I had it :( – rrogers Jan 30 '18 at 20:59
  • There is an alternative method: take f(x) (analytic) and form f(x)/(1-x) , now the coefficient of each term of the power series expansion is the partial sum up to there. This can be obtained analytically, more or less, by taking successive derivatives and setting x=0. – rrogers Jan 30 '18 at 21:04

2 Answers2

10

It’s the formula for the sum of a finite geometric series:

$$\sum_{k=0}^{n-1}x^k=\frac{1-x^n}{1-x}\;,$$

here with $x=\frac13$. Specifically,

$$\sum_{k=1}^n\frac1{3^{k-1}}=\sum_{k=0}^{n-1}\frac1{3^k}=\sum_{k=0}^{n-1}\left(\frac13\right)^k=\frac{1-(1/3)^n}{1-1/3}=\frac32\left(1-\left(\frac13\right)^n\right)=\frac32\left(1-\frac1{3^n}\right)\;.$$

Brian M. Scott
  • 616,228
2

Actually there is a general formula that ends with a twist in your case.

These are all formal/symbol flipping results and may blow up if not used carefully.

The following is a standard result that I repeat because I haven't seen a really elementary proof around.

Theorem 1. Let $f(t)$ be a formal Ordinary Generating function. Then formally the partial sums of the series are generated by $\frac{f(t)}{1-t}$

Proof. We have a OGF function indexed by $t^{i}$ :

$f(t)={\displaystyle \sum_{i=0}^{\infty}a_{i}\cdot t^{i}}$

Write the partial summation formula in t as.

$ F(t)={\displaystyle \sum_{i=0}^{\infty}{\displaystyle t^{i}\cdot\left(\sum_{j=0}^{i}a_{j}\right)}}$

and generate f(t) by subtracting adjacent $t^{i}$ terms .

$\left(1-t\right)\cdot F(t)=\sum_{i=0}^{\infty}{\displaystyle t^{i}\cdot\left(\sum_{j=0}^{i}a_{j}\right)}-\sum_{i=0}^{\infty}{\displaystyle t^{i}\cdot\left(\sum_{j=0}^{i-1}a_{j}\right)=\sum_{i=0}^{\infty}a_{i}\cdot t^{i}=f(t)}$

Thus: $F(t)=\left(\frac{1}{1-t}\right)\cdot f\left(t\right)$ QED

Now in your case we add a parameter $\lambda=\left(\frac{1}{3}\right)$ :

$f(t,\lambda)=\frac{1}{1-\lambda\cdot t}$

$F(t,\lambda)=\frac{1}{1-t}\cdot\frac{1}{1-\lambda\cdot t}$

Which doesn't look like the normal form $\frac{1-\lambda^{n}}{1-\lambda}$ but double checking in Maxima

b:(1/((1-t)(1-lt)));

powerseries(b,t,0);

$\sum_{i=0}^{\infty }\left( -\frac{{l}^{i+1}}{1-l}-\frac{1}{l-1}\right) \,{t}^{i}$

$\frac{1}{1-l}\cdot\sum_{i=0}^{\infty}\left(1-l^{i+1}\right)\cdot t^{i}$

As indeed it must be.

rrogers
  • 986