2

$$\int \sin^4(t)\cos^3(t)dt = \int \sin^4(t)(1-\sin^2(t))\cos(t) dt $$

$$u = \sin(t) \\ du = \cos(t)dt$$

$$ \int \sin^4(t)\cos^3(t)dt = \int u^4(1-u^2) du \\ = u^4 - u^6 = \frac{1}{5}u^5 - \frac{1}{7}u^7 + C \\ = \frac{1}{5}\sin^5(t) - \frac{1}{7}\sin^7(t) + C $$

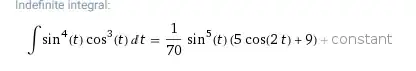
This seems like a simple enough trig substitution integral problem to me. However, when I check my answer with wolphram alpha, it gives: enter image description here
This looks like a simplified version of my answer, but it is not entirely clear to me how it gets reduced down. The furthest I can get is this:

$$ \frac{1}{5}\sin^5(t) - \frac{1}{7}\sin^7(t) = \sin^5(t) \bigg( \frac{1}{5} - \frac{1}{7} sin^2(t) \bigg) \\ = \frac{1}{5}\sin^5(t) \bigg(\frac{1}{5} - \frac{1}{7} \cdot \frac{1}{2} (1 - \cos 2x) \bigg) \\ = \frac{1}{5}\sin^5(t) \bigg(\frac{1}{5} - \frac{1}{14} - \frac{1}{14}\cos 2x\bigg) \\ = \frac{1}{5}\sin^5(t) \bigg(\frac{14}{90} - \frac{5}{90} - \frac{5}{90} \cos 2x \bigg)$$

and I feel like my simplification is not really going anywhere meaningful...

rash
  • 2,060
  • 1
  • 9
  • 28
Evan Kim
  • 2,399

2 Answers2

3

I think your answer is all right since $$\cos 2 \theta =1-2 \sin^2 \theta$$

You see : $$\dfrac{1}{5} \sin^5 (x )+ \dfrac{1}{7} \sin^7 (x) =\dfrac{1}{70} \sin^5( x) (14+10 \sin^2 (x)) =\dfrac{1}{70} (9+5 \cos (2x))$$

MATHS MOD
  • 646
  • 6
  • 14
  • I agree too, I just find it frustrating that wolphram alpha is teasing me by giving me an "answer" and then making me go the extra mile to figure out if it is the same answer or not – Evan Kim Mar 13 '19 at 13:54
  • 1
    @EvanKim Can't be helped, I'm afraid. There's always a chance they'll use a slightly different method from yours, resulting in a different-looking expression that some trigonometric identity makes equal to yours. – J.G. Mar 13 '19 at 13:55
  • 1
    @EvanKim: How can Wolfram Alpha know what your answer looks like? Are you asking it to read your mind? That would be spooky! Like something Google might do. – TonyK Mar 13 '19 at 13:55
  • Someonealign my answer – MATHS MOD Mar 13 '19 at 14:01
  • I realized I could just ask wolphram alpha to "differentiate" my answer, and it turned out to be correct – Evan Kim Mar 13 '19 at 14:04
2

Use the formula $$\int \cos^m(t)\sin^n(t)dt=-\frac{\cos^{m+1}(t)\sin^{n-1}(t)}{m+n}+\frac{n-1}{m+n}\int\cos^m(t)\sin^{n-2}(t)dt$$

Dr. Sonnhard Graubner
  • 95,283