While messing around with the radical center of three circles, I found out the following thing:
Given three circles intersecting in the points $M,N,O,P,Q,R$ as in the picture, the line joining the circumcenters of the triangles $\Delta MNO$, $\Delta PQR$ passes through the radical center of the three circles.
Why is this true? I tried using power of a point wrt the two circles to show that the radical center lies on the line, but to no avail. Any ideas?
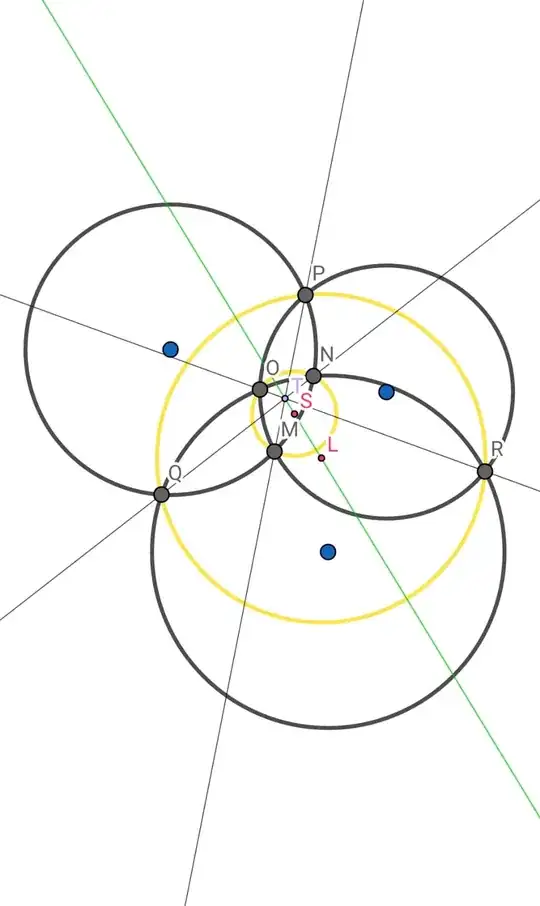
Let $p$ (assumed $<0$) be the common power of the radical center $T$ with respect to the 3 circles.
Consider inversion transform $I$ having $T$ as its center, and $p$ as its power.
$I$ exchanges $M,N,O$ and $P,Q,R$ ; thus, as an inversion sends circles onto circles, (circumscribed) circle $MNO$ is exchanged with (circumscribed) cercle $PQR$.
In such a case the center of inversion is aligned with the circle's centers. QED.
Remarks :
1) In fact, I isn't a "true" inversion, but as Coxeter and Greitzer define it, an anti-inversion, i.e., a composition $I= S \circ I'$, of a genuine inversion $I'$ (with same center $T$, opposite power $-p>0$) and a central symmetry $S$. (see p. 192 of their masterpiece "Geometry Revisited" http://www.aproged.pt/biblioteca/geometryrevisited_coxetergreitzer.pdf). No change in our reasoning because alignment is preserved by $S$.
2) "as circles are sent onto circles" : one could object that a circle could be exchanged with a straight line, but this happens only in the case where the circles pass through the origin, which is not the case here because of assumption $p<0$.
3) I have devoted a question to inversion (Ill-known/original/interesting investigations on/applications of inversion (the geometric transform)) some time ago. A certain number of properties of this transformation can be found there.
