I got this problem from a journal and curious how they have calculated that.Previously I asked this problem and unfortunately did not get any answer. Hereby I am posting again and hopefully someone can answer as it is a popular platform to understand math. Consider I have a sphere that is equally divided into two different patch(gray and white). The total gray portion can be called as Pt The sphere can rotate and translate(up-down) at the air-water interface.
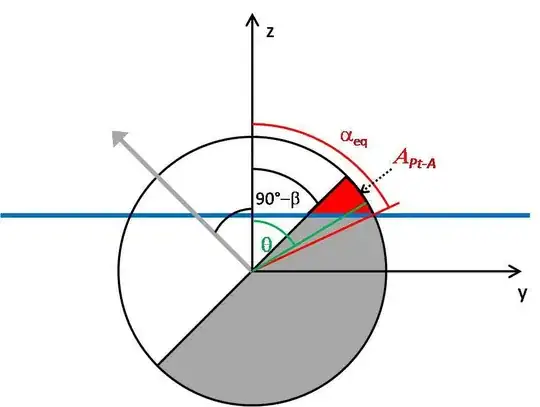 The angle α defines the position of the sphere (alpha increase means the sphere goes towards the air). The angle β defines the rotation of the sphere. So the surface area of any patch into any phase changes with the position and orientation(example: area of Pt inside air phase will change with α and β angle). Now the calculation of the surface area of Pt part of the sphere in air(Apt-A) is given by this equation.
The angle α defines the position of the sphere (alpha increase means the sphere goes towards the air). The angle β defines the rotation of the sphere. So the surface area of any patch into any phase changes with the position and orientation(example: area of Pt inside air phase will change with α and β angle). Now the calculation of the surface area of Pt part of the sphere in air(Apt-A) is given by this equation.
I understand the first integral limit in polar angle direction but did not find out how the limit comes for azimuth angle direction. Please keep in mind that the picture is only visual representation of a 3D sphere in 2D.