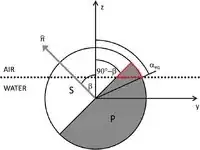
I got this problem and solution in a paper but cannot find how they have solved it. Consider I have a sphere that is equally divided into two different patch(P, S). The sphere can rotate and translate(up-down) at the air-water interface. The angle $\alpha$ defines the position of the sphere (alpha increase means the sphere goes towards the air). The angle $\beta$ defines the rotation of the sphere. So the surface area of any patch into any phase changes with the position and orientation(example: area of P inside air phase will change with $\alpha$ and $\beta$ angle). Now the calculation of the surface area of P part of the sphere in air is given by this equation. I understand the limit for $\theta$ direction but did not find out how the limit comes for $φ$ direction. Here is the visual representation of the problem
Please keep in mind that the figure is only $2D$ presentation of a $3D$ sphere where the coordinate system refers as $(r, θ, φ)$ .