Explanation of a regular pattern only occuring for prime numbers

Question

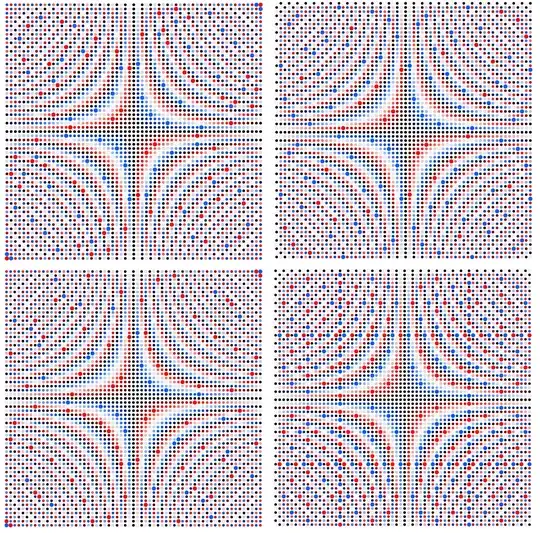
Consider multiplication group tables modulo $n$ with entries $k_{ij} = (i\cdot j)\ \%\ n$ visualized according to these principles:

• Colors are assigned to numbers $0 \leq k \leq n$ from

  • $\color{black}{\textsf{black}}$ for $k=0$ over

  • $\color{red}{\textsf{red}}$ for $k=\lfloor n/4\rfloor$ and

  • $\color{silver}{\textsf{white}}$ for $k=\lfloor n/2\rfloor$ and

  • $\color{blue}{\textsf{blue}}$ for $k=\lfloor 3n/4\rfloor$ back to

  • $\color{black}{\textsf{black}}$ for $k = n$

• Sizes are assigned to numbers $0 \leq k \leq n$ by

  • $\textsf{1.5}$ if $k=\lfloor n/4\rfloor$ or $\lfloor 3n/4\rfloor$

  • $\textsf{1.0}$ otherwise

• Positions are shifted by $(n/2,n/2)$ modulo $n$ to bring $(0,0)$ to the center of the table.

Visualized this way, you will occasionally find (for some $n$) highly regular multiplication group tables like these (with $n=12,20,28,44,52,68$):

My question is:

Why do these patterns occur exactly when $n = 4p$ with a prime number $p$?

---

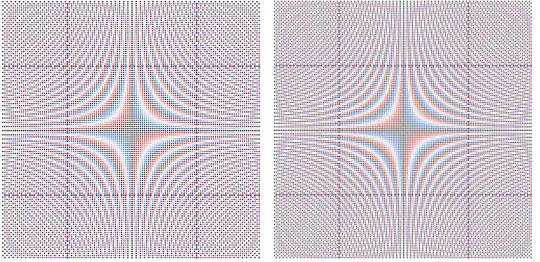
Find here some examples for $n \neq 4p$, e.g. $n=61, 62, 63, 64$:

---

Here for some other prime numbers: $n = 4\cdot 31 = 124$ and $n = 4\cdot 37 = 148$:

---

One may observe that for $n = 4m$ and $x,y = m$ or $x,y = 3m$ the "size 1.5" dots are systematically separated by $0$ (= black) and $n/2$ (= white) dots, i.e. that there are only and exactly $4$ values along these lines.

---

For the sake of completeness: the multiplication group table modulo $8 = 4\cdot 2$ (which also qualifies, but not so obviously):

Answer 1

If $n=4p$, then for $xy \equiv p$ or $3p$ mod $n$ you need $p$ to divide $x$ or $y$ but $2$ to divide neither: thus the "size $1.5$" dots are all on the lines $x = p$, $x = 3p$, $y = p$ and $y = 3p$.

Answer 2

To elaborate a bit on Robert Israels fine answer, first note that: $$ \begin{align} xy&\equiv n/4\\ xy&\equiv 3n/4 \end{align} $$ implies that $n$ must be divisible by $4$. Hence we only have such situations when $n=4q$ for some $q$. This is true whether $q$ is prime or not. So let us consider $n=4q$ a bit further. Then we look at: $$ \begin{align} xy&\equiv q\\ xy&\equiv 3q \end{align} $$ which can be summarized as: $$ xy=q(2m+1) $$ for some $m$. This actually reveals why $n=64=4\cdot 16$ also appears to somewhat work. Here $q=16$ so any solutions to $xy=16(2m+1)$ will work. We have the lines $x,y=\pm2,\pm4,\pm8,\pm16$ with varying density of "size 1.5" points.

When $q$ is prime, the picture becomes simpler since all solutions to $xy=q(2m+1)$ have to lie on one of the four lines $x=\pm q,y=\pm q$.

---

UPDATE: Some insights on the general case here. Write $n=4q+t$ for $t\in\{-1,0,1,2\}$. Then we have: $$ \begin{align} \lfloor n/4\rfloor &= q+\lfloor t/4\rfloor\\ \lfloor 3n/4\rfloor &= 3q+\lfloor 3t/4\rfloor \end{align} $$ where we can make the following table: $$ \begin{array}{c|r|r|r|r} t & -1 & 0 & 1 & 2\\ \hline \lfloor t/4\rfloor & -1 & 0 & 0 & 0\\ \lfloor 3t/4\rfloor & -1 & 0 & 0 & 1 \end{array} $$ and so we can cover each $t$-case based on that.

---

CASE $t=0$

Let us first reconsider the case $t=0$ so that $n=4q$, which was already covered above. Then: $$ xy=q(2\mu+1) $$ will yield "size 1.5" dots. If $q=ab$ is composite then: $$ \begin{align} x&=a\\ y&=b(2\mu+1) \end{align} $$ will yield a vertical line of points $2b$ apart that are all of "size 1.5". If on the other hand $q$ is prime, then: $$ \begin{align} x&=q\\ y&=2\mu+1 \end{align} $$ will yield a very visible vertical line of points only $2$ apart.

---

CASE $t=1$

Suppose $t=1$. Then $n=4q+1$. For this case, having $xy\equiv\lfloor n/4\rfloor=q$ implies: $$ \begin{align} xy &=q+\mu n \end{align} $$ Now, since $q,n$ are relatively prime, $\mu$ must be a multiple of $q$ for two such situations to have any shared factor. So assume $\mu=\gamma q$. Then: $$ xy=(\gamma n+1)q $$ So if $q=ab$ we have: $$ \begin{align} x &= a\\ y &= (\gamma n+1)b \end{align} $$ showing that no vertical lines can exist, since the $y$-values must be far more than $n$ units apart. On the other hand, plugging in $\mu=0$ in the $y$-expression above shows why points tend to lie on the hyperbola: $$ xy=q $$

---

I think the other cases can be broken down in a similar fashion, so I will stop here.