Given a line segment, a line parallel to it, and a straightedge, divide the segment into $n$ equal segments

Question

Given a line segment, a line parallel to it, and a straightedge, how to divide the segment into $n$ equal segments?

(With a straightedge, you are allowed only to draw straight lines. You are not allowed to mark off distances on the straightedge.)

Answer 1

This took a lot of time to finish up. I hope it conveys the interesting nature of this problem. Although the problem is stated quite clearly, it seems to have caused some confusion in the comments and answers, so I will restate it differently:

Given a line segment and a line parallel to it, how can the line segment be partitioned into n equal segments only using a straightedge?

---

Let's start with the $n=2$ case. Let the given line segment be AB, and let the given parallel line be defined with the points $\textbf{F}$ and $\textbf{E}$. Let's name the intersection point of the rays $\textbf{AF}$ and $\textbf{BD}$ as $\textbf{D}$. Let the intersection point of $\textbf{AE}$ and $\textbf{FB}$ be $\textbf{O}$. Let the intersection point of the ray $\mathbf{DO}$ with the line $\textbf{FE}$ be $\mathbf{H_{0}}$. Finally, let the point intersection of the ray $\mathbf{DO}$ and $\textbf{AB}$ be $\mathbf{I_{1}}$. I created a sketch to work on in GeoGebra in the figure below.

Theorem 1

In the following figure, point $\mathbf{I_{1}}$ is the midpoint of $\mathbf{AB}$, ie.: \begin{equation}\label{theorem1} \mathbf{AI_{1}}=\mathbf{I_{1}B}. \end{equation}

The proof of this theorem will use two well-known theorems; namely Thales' Theorem and Ceva's Theorem. Proof. Since $\textbf{AB} \parallel \textbf{FE}$, from Thales' Theorem: $$\tag{1}\label{1} \frac{\textbf{AF}}{\textbf{FD}}=\frac{\textbf{BE}}{\textbf{ED}}$$

From Ceva's Theorem, $$\frac{\textbf{AF}}{\textbf{FD}}\cdot\frac{\textbf{DE}}{\textbf{EB}}\cdot\frac{\mathbf{BI_{1}}}{\mathbf{I_{1}A}}=1$$

Substituting from Eq. $\ref{1}$, $$\mathbf{AI_{1}}=\mathbf{I_{1}B}$$ we obtain the required result. $\blacksquare$

Corollary 1.1

\begin{equation}\tag{2}\label{2} \mathbf{FH_{0}}=\mathbf{H_{0}E} \end{equation} Proof. This can be proved in several different ways. Since Eq.($\ref{1}$) and Eq.($\ref{2}$) were established before, by considering a homothety centered at $\textbf{D}$ it is clear that $\mathbf{FH_{0}}=\mathbf{H_{0}E}$. Alternatively, using the following similar triangles: $\bigtriangleup\mathbf{AI_{1}O} \sim \bigtriangleup\mathbf{EH_{0}O}$ and $\bigtriangleup\mathbf{BI_{1}O} \sim \bigtriangleup\mathbf{FH_{0}O}$, the corollary can be proven. $\blacksquare$

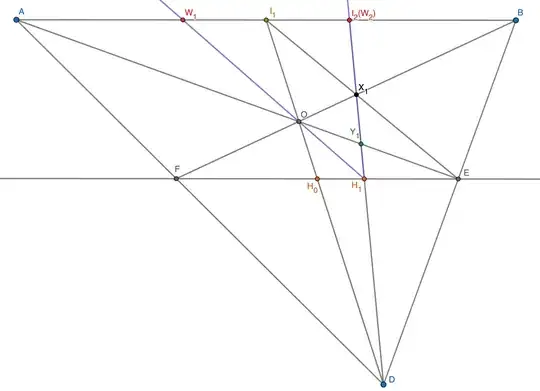Next, for the case $n=3$ (as in the Figure above}, let's connect the points $\mathbf{I_{1}}$ and $\textbf{E}$ and name the intersection of $\mathbf{I_{1}E}$ and $\textbf{FB}$ as $\mathbf{X_{1}}$. Let the point intersection of the ray $\mathbf{DX_{1}}$ and $\textbf{AB}$ be $\mathbf{I_{2}}$. Let the intersection point of the ray $\mathbf{DX_{1}}$ and line segment $\textbf{AE}$ be $\mathbf{Y_{1}}$. Let the intersection point of the ray $\mathbf{DX_{1}}$ with the line $\textbf{FE}$ be $\mathbf{H_{1}}$. Finally, let the intersection points of the line segment $\textbf{AB}$ and the rays $\mathbf{H_{1}O}$, $\mathbf{H_{1}Y_{1}}$ be points $\mathbf{W_{1}}$, $\mathbf{W_{2}}$ respectively. Notice that the ray $\mathbf{H_{1}Y_{1}}$ is contained by the ray $\mathbf{DX_{1}}$, and hence, $\mathbf{I_{2}}$ is coincident with $\mathbf{W_{2}}$. So, the point is labeled as $\mathbf{I_{2}(W_{2})}$. (Alternatively, we could've connected the points $\mathbf{I_{1}}$ and $\textbf{F}$ and name the intersection of $\mathbf{I_{1}F}$ and $\textbf{AE}$ as $\textbf{P}$. Then, we could obtain $\mathbf{W_{1}}$ by finding the intersection of ray $\textbf{DP}$ and $\textbf{AB}$. However, we will stick to the previous method as it is easier to generalize.)

Theorem 2

---

In the figure above, \begin{equation}\tag{3}\label{3} \mathbf{AW_{1}}=\mathbf{W_{1}W_{2}}=\mathbf{W_{2}B} \end{equation}

Proof. Using Eq.(3) and similar triangles in Figure 2 , Theorem 2 can be proven. \begin{equation}\tag{4}\label{4} \bigtriangleup\mathbf{I_{1}X_{1}B} \sim \bigtriangleup\mathbf{EX_{1}F} \;and \bigtriangleup\mathbf{I_{1}X_{1}W_{2}} \sim \bigtriangleup\mathbf{EX_{1}H_{1}} \implies \frac{\mathbf{I_{1}B}}{\mathbf{2FH_{O}}}=\frac{\mathbf{I_{1}W_{2}}}{\mathbf{H_{1}E}} \end{equation}

\begin{equation}\tag{5}\label{5} \bigtriangleup\mathbf{AOW_{1}} \sim \bigtriangleup\mathbf{EOH_{1}} \;and \bigtriangleup\mathbf{W_{1}OI_{1}} \sim \bigtriangleup\mathbf{H_{1}OH_{0}} \implies \frac{\mathbf{AW_{1}}}{\mathbf{H_{1}E}}=\frac{\mathbf{W_{1}I_{1}}}{\mathbf{H_{0}H_{1}}} \end{equation}

\begin{equation}\tag{6}\label{6} \bigtriangleup\mathbf{I_{1}OB} \sim \bigtriangleup\mathbf{H_{0}OF} \;and \bigtriangleup\mathbf{W_{1}OI_{1}} \sim \bigtriangleup\mathbf{H_{1}OH_{0}} \implies \frac{\mathbf{I_{1}B}}{\mathbf{FH_{O}}}=\frac{\mathbf{W_{1}I_{1}}}{\mathbf{H_{0}H_{1}}} \end{equation}

Combining Eq.(5), Eq.(6), and Eq.(7), we get $\mathbf{AW_{1}}=\mathbf{2{I_{1}W_{2}}}$. By the symmetry of the figure, it is also true that, $\mathbf{W_{2}B}=\mathbf{2{W_{1}I_{1}}}$. Combining the two results with Eq. (1), $\mathbf{AW_{1}}=\mathbf{W_{1}W_{2}}=\mathbf{W_{2}B}. \; \blacksquare$

The proof for Theorem Theorem 2 using similar triangles can be extended to construct proofs for the rest of the theorems that will be deduced (for Theorem 3 and Theorem 4). Before trying to generalize, let's also analyze the case for $n=4$ in Figure below. Similar to what we did for the $n=3$ case let's connect the points $\mathbf{I_{2}}$ and $\textbf{E}$ and name the intersection of $\mathbf{I_{2}E}$ and $\textbf{FB}$ as $\mathbf{X_{2}}$. Let the point intersection of the ray $\mathbf{DX_{2}}$ and $\textbf{AE}$ be $\mathbf{Y_{2}}$. Let the intersection point of the ray $\mathbf{DX_{2}}$ with the line $\textbf{FE}$ be $\mathbf{H_{2}}$. Let the intersection points of the line segment $\textbf{AB}$ and the rays (purple) $\mathbf{H_{2}O}$, $\mathbf{H_{2}Y_{1}}$, and $\mathbf{H_{2}Y_{2}}$ be points $\mathbf{W_{1}}$, $\mathbf{W_{2}}$, $\mathbf{W_{3}}$ respectively. Note that $\mathbf{I_{1}}$ is coincident to $\mathbf{W_{2}}$ and $\mathbf{I_{3}}$ is coincident to $\mathbf{W_{3}}$.

Theorem 3

---

In the figure above, \begin{equation}\tag{7}\label{7} \mathbf{AW_{1}}=\mathbf{W_{1}W_{2}}=\mathbf{W_{2}W_{3}}=\mathbf{W_{4}B} \end{equation}

The same methodology can be applied repeatedly to obtain solutions for all values of ${\textit{n}}$. Let the intersection points of the line segment $\textbf{BF}$ with the rays $\mathbf{DH_{1}, DH_{2}, DH_{3},...,DH_{n-2}}$ be called as $\mathbf{X_{1}, X_{2}, X_{3}, ..., X_{n-2}}$. Let the intersection points of the rays $\mathbf{DO, DX_{1}, DX_{2}, ..., DX_{n-2}}$ with the line $\textbf{FE}$ be $\mathbf{H_{0}, H_{1}, H_{2}, ..., H_{n-2}}$. Then, let's name the intersection points of the rays $\mathbf{DO, DX_{1}, DX_{2}, ..., DX_{n-2}}$ with the line segment $\textbf{AB}$ as $\mathbf{I_{1}, I_{2}, I_{3}, ..., I_{n-1}}$. Let's form the rays $\mathbf{H_{n-2}O, H_{n-2}Y_{1}, H_{n-2}Y_{2}, ... , H_{n-2}Y_{n-2}}$ and name the intersection points of these rays with $\textbf{AB}$ as $\mathbf{W_{1}, W_{2}, W_{3}, ..., W_{n-1}}$. Voil'a, the line segment $\textbf{AB}$ is partitioned into $\textit{n}$ equal segments. As a final note, $\forall \; (k+1)|n$, $\mathbf{I_{k}}$ is coincident to $\mathbf{W_{m}}$ for certain values of $\textbf{m}$.

Theorem 4

---

In general, \begin{equation}\tag{8}\label{8} \mathbf{AW_{1}}=\mathbf{W_{1}W_{2}}=\mathbf{W_{2}W_{3}}=\mathbf{W_{3}W_{4}}=...=\mathbf{W_{n-1}B} \end{equation}

Let's illustrate it with an example. Suppose, we are trying to divide $\textbf{AB}$ into six equal segments. Thus, in this case $n=6$, and we can use the general method we derived. Applying the method discussed above, the figure below can be obtained. Notice the labeling of the following points: $\mathbf{I_{1}(W_{3})}, \mathbf{I_{2}(W_{4})}, \mathbf{I_{5}(W_{5})}$. As stated above, this coincidence occurs because 2, 3, and 6 are factors of 6.

Answer 2

Partial Answer

Here's a solution for the case $n = 2$, which might provide you some inspiration for the more general case. The picture tells the whole story. The red line $PQ$ is the initial segment, the blue line is the parallel one. We pick points $A$ and $B$ on the blue line at random. We join each of $A$ and $B$ to each end of the initial segment. The lines $PA$ and $QB$ intersect at the magenta point; the lines $PB$ and $QA$ intersect at the blue point, and joining the blue and magenta points and taking the intersection with the original line $PQ$ gives us the red point, which is the midpoint of $PQ$.

Note that I did need to assume I could pick two distinct points on a given line; I'm not certain that this is allowed in straightedge-only constructions.

Clearly this solution generalizes to handle all cases where $n$ is a power of $2$ (just apply recursively to sub-lines), but I don't see how to do $n = 3$; presumably once that's clear, the rest is downwind sailing.

Answer 3

Hint. Assuming you are allowed a compass...

It might seem hard to divide the given line $n$ times but you can take the parallel line; extend it $n$ times to get a parallel line that is $n$ times longer than it was originally and you have successfully divided that big new line in $n$ equal parts.

Is there any way to take those $n$ parts an the parallel line to make $n$ equal parts of the original line?

What do you know about parallel lines, and equal angles, and similar triangles?

Time to brainstorm....

......