using diagonals of the a trapezoid inside a triangle you can find the midpoint of the bases

Question

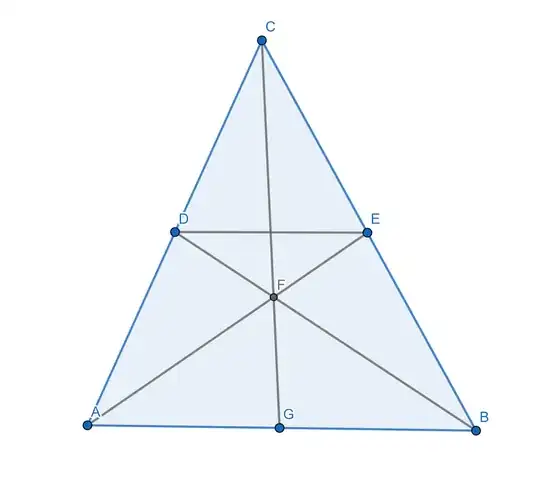
In the following triangle, AB is parallel to DE. F is an intersection point of the segments BD, AE and CG. Is it true that AG = GB?

Answer 1

In the following, I have incorrectly assumed D and E are the midpoints of CA and CB respectively. Please jump right to the section labeled as "CORRECTED version".

We can play withit using areas. The respective regions are labelled as shown.

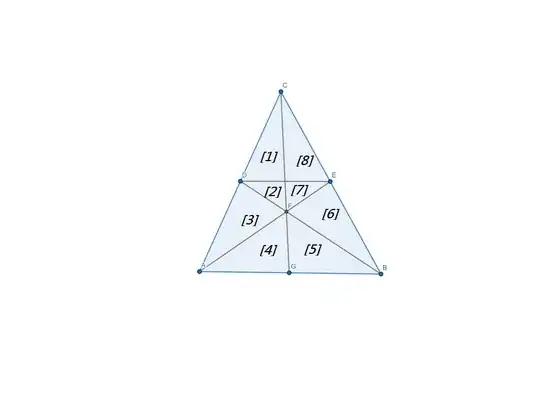
(1) + (2) = (3) = (6) = (8)+ (7)

∴ (1) + (2) + (3) = (6) + (8)+ (7) = x, say

$\dfrac {x + (4)}{x +(5)} = \dfrac {(4)}{(5)}$

This gives (4) = (5) and the required result follows

---

CORRECTED version

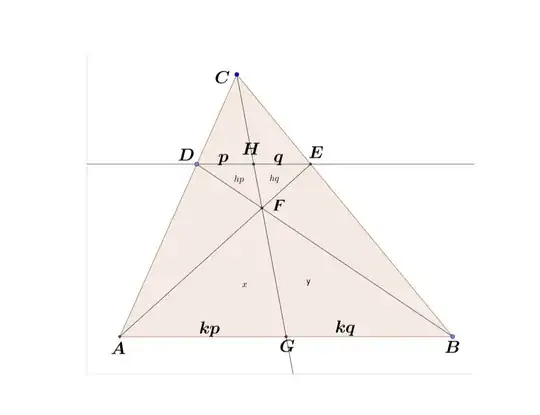
Let C(F)G cut DE at H. Suppose that DH : HE = p : q.

Then, (1) by similar triangles, AG = kp and GB = kq for some non-zero constant k; (2) by triangles with the same altitude, [FDH] = hp and [FEH] = hq for some non-zero constant h.

Let [AFG] = x and [BFG] = y. Then, by considering areas of similar objects, $x = hq \times (\dfrac {kp}{q})^2$ and $y = hp \times (\dfrac {kq}{p})^2$.

Therefore, $\dfrac {x}{y} = … = (\dfrac {p}{q})^3$

Since, by considering area of triangles with the same altitude, $\dfrac {x}{y} = \dfrac {kp}{kq}$

From $(\dfrac {p}{q})^3 = \dfrac {kp}{kq}$, we have $p = q$ after rejecting the negative quantities.

Answer 2

Yes, use Ceva Theorem: $${AG\over GB}\cdot {BE\over EC}\cdot {CD\over DA}=1$$ and Thales theorem: $${CD\over DA} = {EC\over BE} $$ and thus a conclusion.