0

As we all know, the sequence $1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n$ is decreasing and bounded. Its limit is called Euler constant denoted by $\gamma$. I can get $$0<1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n<1.$$ And if we use the limit $\gamma=0.577~215\cdots$, we know $$1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n>\frac{1}{2}.$$ Now my question is how to prove $$1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n>\frac{1}{2}$$ without the properties of limit and $\gamma=0.577~215\cdots$.

Riemann
  • 7,203
  • Estimate Riemann sums, perhaps? Note $\log n = \int_{[1,n]} \frac{dt}{t}$. – MathematicsStudent1122 Jan 16 '19 at 06:27
  • $f(n) = \sum_{k=1}^n \frac1k - \log(n+1)$ is increasing it converges to $\gamma$ and $f(6) \approx 0.504$ – reuns Jan 16 '19 at 07:08
  • For rough estimates on convex/concave functions, you may be able to get by with using secant lines or tangent lines to create lower bounds. Using osculatory quadratics isn't something I'd recommend doing, but if nothing else comes to mind you might try it. –  Jan 16 '19 at 07:20
  • Thank you very much! But I want a method without calculus, only knowledge of high school. @ Robert Wolfe – Riemann Jan 16 '19 at 07:23

2 Answers2

3

Any other elementary proof will welcome.

I get an idea from Showing $\gamma < \sqrt{1/3}$ without a computer

$$\gamma = \int_{0}^{+\infty}\left(\frac{1}{1-e^{-x}}-\frac{1}{x}\right)e^{-x}\,dx.\tag{1}$$ Since $f(x)=\frac{1}{1-e^{-x}}-\frac{1}{x}$ is concave on $\mathbb{R}^+$, for any $x\in\mathbb{R}^+$ we have $f(x)>\frac{1}{2}$, so: $$\gamma>\int_{0}^{+\infty}\frac{1}{2}e^{-x}\,dx = \frac{1}{2}.$$ By the same way, $f(x)>\frac{1}{2}+\frac{1}{2}x-\frac{1}{720}x^3$, $$\gamma>\int_{0}^{+\infty}\left(\frac{1}{2}+\frac{1}{2}x-\frac{1}{720}x^3\right)e^{-x}\,dx = \frac{23}{40}=0.575.$$ 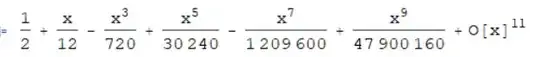enter image description here The Taylor expansion of $f(x)$.

Riemann
  • 7,203
2

For integer $n > 1$, $\log n$ is the area below the curve $y = 1/x$ for $1 \le x \le n$. If we estimate this area by the trapezium rule, the result will be an over-estimate because the graph of $y = 1/x$ lies below its chords. Hence $$\log n < {1\over2}\left({1\over1}\right) + {1\over2} + {1\over 3} + \cdots + {1\over{n-1}} + {1\over2}\left({1\over n}\right),$$ which gives $$1 + {1\over 2} + \cdots + {1\over n} - \log n > {1\over 2} + {1\over 2n}.$$

Michael Behrend
  • 1,345