Compute volume of parallelepiped using triple vector

Question

Before anyone claims that I am not studying, my university recently changed their coursework that does not require linear algebra as a pre-requisite to multi-variable calculus.

My professor gave us these questions even though we have no experience with matrix, he did not even teach us about it and I had to study them online by myself.

I only got as far as I could and I only want one question help so I can work on the other similar questions by myself. I would not be here if I can't find any other help.

Two very basic operations from multivariable calculus that you should know are the cross product of two vectors, and the dot product of two vectors. To calculate the volume of the parallelepiped, you need to compute $(\vec{\bf a} \times \vec{\bf b})\cdot{\bf c}$ (known as the scalar triple product). — Decaf-Math, Jan 11 '19 at 05:44
@LordSharktheUnknown the area of the parallelogram of vector a and b. Which I got to as /sqrt(20). but I think the more relevant thing is the cross product of vector a and b, which is 4j -2k.
(can someone tell me where I can format?) — Zealotory, Jan 11 '19 at 06:42
The area of the parallelogram formed by $\vec a,\vec b$ is the magnitude of the vector $\vec a\times\vec b$. Now, the volume of a parallelopiped is given by the base area times the height, where the height is the absolute projection of $\vec c$ along the base areal vector $\vec a\times\vec b$ — Shubham Johri, Jan 11 '19 at 06:53
@ShubhamJohri thanks, you worded it a lot easier for me to understand the material. — Zealotory, Jan 11 '19 at 07:04
Can someone help me confirm? My answer turned out to be -6. I think I am wrong since my answer is negative. — Zealotory, Jan 11 '19 at 07:07
My math shows the vectors are coplanar. I think I'm doing something wrong... — Christopher Marley, Jan 11 '19 at 07:17
@JowieTan Do you mean $(\vec a\times\vec b)\cdot\vec c=-6$? The answer should be $0$, check again. — Shubham Johri, Jan 11 '19 at 07:23
@JowieTan The result of the vector computation can be positive or negative. If it's negative, then the volume is the absolute value of it. — Angina Seng, Jan 11 '19 at 07:25
I am retarded, I used the wrong ($\vec a * \vec b$) from question 2 — Zealotory, Jan 11 '19 at 07:30

score 1 · Answer 1 · edited Jul 07 '20 at 14:35

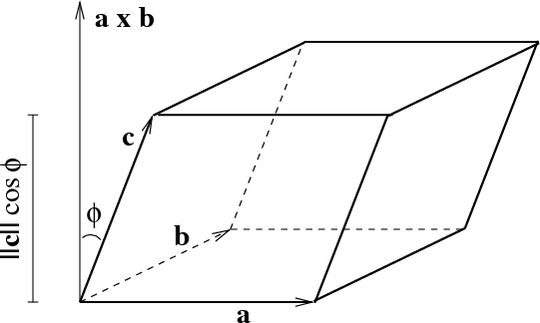
The volume of the parallelepiped is the base area times the height. The base area, as you know, is the magnitude of $\vec a\times\vec b$, that is $\|\vec a\times\vec b\|$.

You also know that $\vec a\times\vec b$ is a vector perpendicular to the plane containing $\vec a,\vec b$. Thus, the height of the parallelepiped is the absolute value of the projection of $\vec c$ along $\vec a\times\vec b$, that is $\Big|\vec c\cdot\frac{\vec a\times\vec b}{\|\vec a\times\vec b\|}\Big|$ (for the derivation of this quantity, see this answer).

Multiply them together to get$$V=\Big|\vec c\cdot\frac{\vec a\times\vec b}{\|\vec a\times\vec b\|}\Big|\|\vec a\times\vec b\|=|\vec c\cdot\vec a\times\vec b|$$

$\vec c\cdot\vec a\times\vec b$ is called the scalar triple product of vectors $\vec a,\vec b,\vec c$ and denoted as $[\vec a\ \vec b\ \vec c]$. The volume of the parallelepiped formed by three vectors is the geometrical interpretation of the absolute value of their scalar triple product.

In your case, note that $\vec a,\vec b,\vec c$ are coplanar, as $\vec b-\vec c=\vec a$. The volume of the parallelepiped formed by three vectors lying in the same plane is zero. You can verify the same using scalar triple product.

Compute volume of parallelepiped using triple vector

1 Answers1

Linked