What is the expected number of randomly generated numbers in the range [a, b] required to reach a sum $\geq X$?

Question

We are generating random numbers (integers) in the range $[a, b]$. All values are equally likely.

We will continue to generate random numbers in this range, and add up successive values until their combined sum is greater than or equal to a set number $X$.

What is the expected number of rolls to reach at least $X$?

Example:

a = 1000
b = 2000
X = 5000

Value 1: 1257 (total sum so far = 1257)
Value 2: 1889 (total sum so far = 3146)
Value 3: 1902 (total sum so far = 5048; all done)

So it took $3$ rolls to reach $\geq5000$. Intuitively, we can say that it will not take more than $5$ rolls if each roll is $1000$. We can also say that it will not take less than $3$ rolls if each roll was $2000$. So it stands to reason that in the example above, the expected number of rolls lies somewhere between $3$ and $5$.

How would this be solved in the general case for arbitrary values $[a, b]$ and $X$? It's been quite a while since I last took statistics, so I've forgotten how to work with discrete random variables and expected value.

Answer 1

Let $T$ be the number of times it takes to reach $X$. We compute $E[T]$ via $E[T]=\sum_{t=0}^\infty P(T>t)$.

In order to have $T>t$, the sum of the first $T$ samples needs to be less than $X$. Let $S_i$ be the value of the $i^{th}$ sample. Then an experiment where $T>t$ has the first $t$ values satisfying $$ S_1+S_2+\dots+S_t<X,\\ a\le S_i\le b $$ Letting $E=X-1-(S_1+\dots+S_t)$, we get $$ S_1+\dots+S_t+E=X-1,\\ a\le S_i\le b,\\ E\ge 0 $$ The number of integer solutions to the above system of equations and inequalities in the variables $S_i$ and $E$ can be computed via generating functions. The number of solutions is the coefficient of $s^{X-1}$ in $$ (s^a+s^{a+1}+\dots+s^b)^t(1-s)^{-1}=s^{at}\cdot(1-s^{b-a+1})^t(1-s)^{-(t+1)} $$ After a bunch of work, this coefficient is equal to $$ \sum_{k=0}^{\frac{X-1-ta}{b-a+1}} (-1)^k\binom{t}k\binom{t+X-1-ta-(b-a+1)k}{t} $$ Finally, we get \begin{align} E[T] &=\sum_{t=0}^{X/a} P(T>t) \\&=\boxed{\sum_{t=0}^{X/a} (b-a+1)^{-t}\sum_{k=0}^{\frac{X-1-ta}{b-a+1}}(-1)^k\binom{t}k\binom{t+X-1-ta-(b-a+1)k}{t}} \end{align} Note that when $a=0$, the summation in $t$ will go from $t=0$ to $\infty$, so it can only be computed approximately with a computer. However, this caveat can be avoided using the following observation; if $T(a,b,X)$ is the expected time to reach $X$ using sums of $\operatorname{Unif}\{a,a+1,\dots,b\}$ random variables, then $E(T(0,b,X))=\frac{b+1}bE(T(1,b,X))$.

When I write $\sum_{k=0}^a f(k)$ and $a$ is not an integer, what I mean is $\sum_{k=0}^{\lfloor a \rfloor}f(k)$.

Answer 2

All right, now that rigorous argument I alluded to. Credit to the late Kent Merryfield for laying out the argument cleanly, although I'm sure I contributed in the development stage. AoPS link

Suppose we add independent copies of a reasonably nice nonnegative continuous random variable with density $f$, mean $\mu$, and variance $\sigma^2$ until we exceed some fixed $y$. As $y\to\infty$, the expected number $g(y)$ of these variables needed to exceed $y$ is $$g(y)=\boxed{\frac{y}{\mu}+\frac12+\frac{\sigma^2}{2\mu^2}+o(1)}$$ In the case of the uniform $[a,b]$ distribution of this problem, that is $g(y)=\frac{2y}{a+b}+\frac12+\frac{(b-a)^2}{6(b+a)^2}+o(1)$.

To prove this, condition on the first copy of the variable. If it has value $x$, the expected number of additional terms needed is $g(y-x)$. Add the one for the term we conditioned on, integrate against the density, and $$g(y)=1+\int_0^y f(x)g(y-x)\,dx$$ This is a convolution. To resolve it into something we can work with more easily, apply a transform method. Specifically, in this case with a convolution over $[0,\infty]$, the Laplace transform is most appropriate. If $F(s)=\int_0^{\infty}e^{-sx}f(x)\,dx$ and $G(s)=\int_0^{\infty}e^{-sy}g(y)\,dy$, then, transforming that integral equation for $g$, we get $$G(s)=\frac1s+F(s)G(s)$$ Solve for $G$, and $$G(s)=\frac1{s(1-F(s))}$$ Now, note that $F$ is essentially the moment-generating function for the variable with density $f$; there's a sign change, but it's otherwise the same. As such, it has the power series expansion $$F(s)=1-\mu s+\frac{\mu^2+\sigma^2}{2\mu^2}s^2 + O(s^3)$$ near zero. Then $$G(s)=\frac1{\mu s^2-\frac{\mu^2+\sigma^2}{2}s^3+O(s^4)} = \frac1{\mu}s^{-2}+\frac{\mu^2+\sigma^2}{2\mu^2}s^{-1}+Q(s)$$ where $Q(s)$ has a removable singularity at zero. Also, from the "reasonably nice" condition, $Q$ decays at $\infty$ How fast? Well, as long as the density of $f$ is bounded above by some exponential, its transform $F$ goes to zero as $s\to\infty$. Then $G(s)=\frac1{s(1-F(s)}=O(s^{-1})$ as $s\to\infty$; subtracting off the two other terms, $Q(s)=O(s^{-1})$ as $s\to\infty$.

Now, we take the inverse Laplace transform of $G$. The inverse transform of $s^{-2}$ is $y$ and the inverse transform of $s^{-1}$ is $1$, so there's the $\frac{y}{\mu}+\frac{\sigma^2+\mu^2}{2\sigma^2}$ terms of the expansion of $g$. For the remainder $Q$, we bring out the integral formula $q(y)=\frac1{2\pi}\int_{\infty}^{\infty}Q(it)e^{ity}\,dt$. Again for nice enough $f$ - a square-integrable density will do - this decays to zero as $y\to\infty$ (Riemann-Lebesgue lemma).

And now, it's time to get more concrete. Our original example was a uniform distribution on $[a,b]$, which has mean $\mu=\frac{a+b}{2}$ and variance $\sigma^2=\frac{(b-a)^2}{12}$. That gives $$g(y)=\boxed{\frac{2y}{a+b}+\frac12+\frac{(b-a)^2}{6(a+b)^2}+o(1)}$$ Also, we can be more explicit; the transforms are $F(s)=\frac1{(b-a)s}(e^{-as}-e^{-bs})$ and $$G(s)=\frac{1}{s-\frac1{b-a}e^{-as}+\frac1{b-a}e^{-bs}}$$ This $G$ is analytic in the right half-plane except for the pole at zero, and is comparable to $\frac1s$ at $\infty$ in all directions in that half-plane. The remainder term $Q$ is thus smooth and decays like $\frac1s$ along the imaginary axis, so its inverse transform $q$ will have a jump discontinuity (at zero, where it goes from zero to $1$) and decay rapidly.

If we want an explicit form for $g$ - it's a mess. Three different exponentials in that denominator pushes this far off the standard tables of transforms, and splitting it up as a geometric series introduces way too many terms. I'll try to write something down anyway: \begin{align*}G(s) &= \frac{1}{s-\frac1{b-a}e^{-as}+\frac1{b-a}e^{-bs}}\\ &= s^{-1} +\frac{s^{-2}}{b-a}\left(e^{-as}-e^{-bs}\right)+\frac{s^{-3}}{(b-a)^2}\left(e^{-as}-e^{-bs}\right)^2+\cdots\\ &= \sum_{n=0}^{\infty} \frac{s^{-n-1}}{(b-a)^n}\left(e^{-as}-e^{-bs}\right)^n\\ &= \sum_{n=0}^{\infty}\sum_{k=0}^n\frac{s^{-n-1}}{(b-a)^n}\binom{n}{k}(-1)^k e^{-s(kb+(n-k)a)}\end{align*} Now, in the table of Laplace transforms I'm using, there's an entry "delayed $n$th power with frequency shift"; the transform of $(y-\tau)^n e^{-\alpha(y-\tau)}u(y-\tau)$ (where $u$ is the unit step function) is $n!e^{-\tau s}(s+\alpha)^{-n-1}$. From this and the linearity of the transform, we get $$g(y) = \sum_{n=0}^{\infty}\sum_{k=0}^n[y-(kb+(n-k)a)]^n\frac{(-1)^k}{k!(n-k)!}u[t-(kb+(n-k)a)]$$ $$g(y) = \sum_{j=0}^{\infty}\sum_{k=0}^{\infty} (-1)^k\frac{[y-(ja+kb)]^{j+k}}{j!k!}u[t-(kb+(n-k)a)]$$ For any given $y$, this is a finite sum; we only sum those terms for which $ja+kb \le y$. It is horrible to use in practice, since it involves adding and subtracting large numbers to get something relatively small.

The $a=0$ case allows us to split things up differently, and comes out with something that's actually reasonably practical. Follow the link at the start of the post if you want to see it.

Answer 3

The expected number is dominated by the term based on the mean $\frac{2X}{a+b}$ - but we can do better than that. As $X\to\infty$, $$E(n) = \frac{2X}{a+b}+\frac{2(a^2+ab+b^2)}{3(a^2+2ab+b^2)}+o(1)$$ Why? Consider the excess. In the limit $X\to\infty$, the frequency of hitting a particular point approaches a uniform density of $\frac{2}{b+a}$. For points in $[X,X+a)$, this is certain to be the first time we've exceeded $X$, so the density function for that first time exceeding $X$ is approximately $\frac{2}{b+a}$ on that range. For $t\in[X+a,X+b)$, the probability that it's the first time exceeding $X$ is $\frac{X+b-t}{b-a}$; we need the last term added to be at least $t-X$. Multiply by $\frac{2}{b+a}$, and the density function for the first time exceeding $X$ is approximately $\frac{2(X+b-t)}{b^2-a^2}$ on $[X+a,X+b)$. For $t<X$ or $t\ge X+b$, of course, the density is zero. Graphically, this density is a rectangular piece followed by a triangle sloping to zero. Now, the expected value of the first sum to be greater than $X$ is approximately $$\int_{X}^{X+a}\frac{2t}{b+a}\,dt+\int_{X+a}^{X+b}\frac{2t(X+b-t)}{b^2-a^2}\,dt$$ $$=\frac{2a(2X+a)}{2(b+a)}+\frac{2(b-a)(2X+a+b)(X+b)}{2(b^2-a^2)}-\frac{2(b-a)((X+a)^2+(X+a)(X+b)+(X+b)^2)}{3(b^2-a^2)}$$ $$=\frac{6aX+3a^2+6X^2+3(a+3b)X+3ab+3b^2-6X^2-6(a+b)X-2(a^2+ab+b^2)}{3(b+a)}$$ $$=\frac{3(a+b)X+a^2+ab+b^2}{3(b+a)}=X+\frac{a^2+ab+b^2}{3(a+b)}$$ Divide by the mean $\frac{a+b}{2}$ of each term in the sum, and we have an asymptotic expression for $E(n)$.

This is not a rigorous argument. If I wanted to do that, I'd bring out something like the moment-generating function.

Answer 4

Given $m$ discrete variables in the range $[a,b]$, the number of ways to get a sum $s$ out of them corresponds to $$ \eqalign{ & N_b (s - ma,d,m) = \cr & = {\rm No}{\rm .}\,{\rm of}\,{\rm solutions}\,{\rm to}\;\left\{ \matrix{ a \le {\rm integer}\;y_{\,j} \le b \hfill \cr y_{\,1} + y_{\,2} + \; \cdots \; + y_{\,m} = s \hfill \cr} \right.\quad = \cr & = {\rm No}{\rm .}\,{\rm of}\,{\rm solutions}\,{\rm to}\;\left\{ \matrix{ {\rm 0} \le {\rm integer}\;x_{\,j} \le b - a = d \hfill \cr x_{\,1} + x_{\,2} + \; \cdots \; + x_{\,m} = s - ma \hfill \cr} \right. \cr} $$ where $N_b$ is given by $$ \bbox[lightyellow] { N_b (s-ma,d,m)\quad \left| {\;0 \leqslant \text{integers }s,m,d} \right.\quad = \sum\limits_{\left( {0\, \leqslant } \right)\,\,k\,\,\left( { \leqslant \,\frac{s-ma}{d+1}\, \leqslant \,m} \right)} {\left( { - 1} \right)^k \binom{m}{k} \binom { s -ma+ m - 1 - k\left( {d + 1} \right) } { s-ma - k\left( {d + 1} \right)}\ } } \tag{1} $$ as widely explained in this post.
Let's also notice the symmetry property of $N_b$ $$ N_b (s - ma,d,m) = N_b (md - \left( {s - ma} \right),d,m) = N_b (mb - s,d,m) $$

The probability of obtaining exactly the sum $s$ in $m$ rolls is therefore $$ \bbox[lightyellow] { \eqalign{ & p(s\;;\,m,a,b) = {{N_b (s - ma,d,m)} \over {\left( {d + 1} \right)^{\,m} }} = {{N_b (mb - s,d,m)} \over {\left( {d + 1} \right)^{\,m} }} = \cr & = {1 \over {\left( {d + 1} \right)^{\,m} }} \sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{{s - ma} \over {d + 1}}\, \le \,m} \right)} { \left( { - 1} \right)^k \binom{m}{k} \binom{ s -ma+ m - 1 - k\left( {d + 1} \right) }{ s-ma - k\left( {d + 1} \right)} } = \cr & = {1 \over {\left( {d + 1} \right)^{\,m} }} \sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{{mb - s} \over {d + 1}}\, \le \,m} \right)} { \left( { - 1} \right)^k \binom{m}{k} \binom{ mb-s+ m - 1 - k\left( {d + 1} \right) }{ mb-s - k\left( {d + 1} \right)} } \cr} } \tag{2} $$ and the sum of $p$ over $s$ is in fact one.

The probability $p$ quickly converges, by Central Limit Theorem, to the Gaussian in the variable $s$ $$ \cal N\left( {\mu ,\sigma ^{\,2} } \right)\quad \left| \matrix{ \;\mu = m\left( {{d \over 2} + a} \right) = m\left( {{{a + b} \over 2}} \right) \hfill \cr \;\sigma ^{\,2} = m{{\left( {d + 1} \right)^{\,2} - 1} \over {12}} \hfill \cr} \right. $$ see for instance this post.

It is easy to demonstrate (by the "double convoluton" of binomials) that the Cumulative version, i.e. the probability to obtain a sum $\le S$, is $$ \bbox[lightyellow] { \eqalign{ & P(S\;;\,m,a,b) = {1 \over {\left( {d + 1} \right)^{\,m} }}\sum\limits_{0\, \le \,\,s\,\, \le \,S} {N_b (s - ma,d,m)} = \cr & = {1 \over {\left( {d + 1} \right)^{\,m} }}\sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{{s - ma} \over {d + 1}}\, \le \,m} \right)} { \left( { - 1} \right)^k \binom{m}{k} \binom{S - ma + m - k\left( {d + 1} \right) }{S - ma - k\left( {d + 1} \right) } } \cr & \approx {1 \over 2}\left( {1 + {\rm erf}\left( {\sqrt 6 {{S + 1/2 - m\left( {a + b} \right)/2} \over {\left( {b - a + 1} \right)\sqrt m \;}}} \right)} \right) \cr} } \tag{3} $$

The following plot allows to appreciate the good approximation provided by the asymptotics even at relatively small values of the parameters involved.

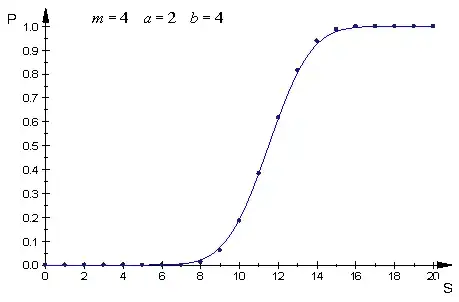
That premised,
the probability that we reach or exceed a predefined sum $X$ at the $m$-th roll and not earlier
is given by the probability that
we get $S<X$ as the sum of the first $m-1$ rolls, and then that the $m$-th one has a value $s$ such that $X \le S+s$,
or, what is demonstrably the same, by
the probability of getting $X \le S$ in $m$ rolls minus the probability of getting the same in $m-1$ rolls.

That is, in conclusion $$ \bbox[lightyellow] { \eqalign{ & Q(m\;;\,X,a,b)\quad \left| \matrix{ \;1 \le m \hfill \cr \;0 \le X \hfill \cr \;0 \le a \le b \hfill \cr} \right.\quad = \cr & = 1 - P(X - 1\;;\,m,a,b) - 1 + P(X - 1\;;\,m - 1,a,b) = \cr & = P(X - 1\;;\,m - 1,a,b) - P(X - 1\;;\,m,a,b) \cr} } \tag{4} $$ and the sum of $Q$ over $m$ correctly checks to one.

Example

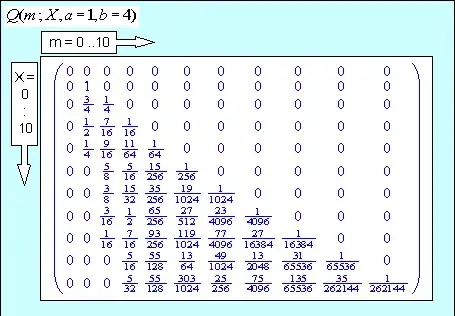
a) For small values of $X,a,b$ the exact expression for $Q$ in (4) gives the results shown (e.g. $a=1, \; b=4$) which look to be correct and the row sums correctly check to be $1$.

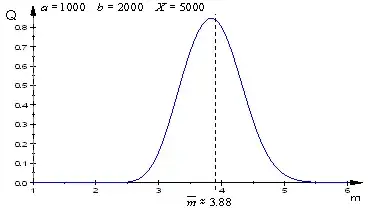
b) For large values of the parameters, like in your example $a=1000,\; b=2000, \; X=5000$ we shall use the asymptotic version of $Q$ which gives the results plotted below