expected value of minimum of sum random variable uniformly distributed variables

Question

Let $U_1$, $U_2$, $U_3$... random variables uniformly distributed over the interval [0,1]. Define $n(x)$ as $n(x)$= $\min$ $\{$$n$| $\sum_1^n$ $U_i>x$$\}$. I need to find $\Bbb E[n(x)]$ I tried to find $\Bbb E[n(x)]$ conditioning on the value of $U_1$ than i use the fact $\tag{2}\Bbb E \left[ n(x) | U_1=y\right] = \cases{1,& $y>x$\cr 1+\Bbb E(x-y),& $y\le x $}.$ but I'm struggling to build the integral, I don't know how to proceed any further than that. I appreciate any help. Thank you in advance.

Answer 1

For the sake of notation, let's denote $U_0 =0$. The probability of the event $\{n(x)=k \}$ for $k\in \mathbb{N^*}$ is \begin{align} P(n(x)=k) &= P(\{\sum_{i=0}^{k-1}U_k<x\}\cap \{\sum_{i=0}^{k}U_k \ge x \}) \\ &= P(\{S_k-U_k<x\}\cap \{S_k \ge x \}) \\ \end{align} with $S_k$ defined as $S_k=\sum_{i=0}^{k}U_k$.

We have $S_k$ follows the Irwin-Hall distribution with the density function $f(s;k)$. Hence \begin{align} P(n(x)=k) &= P(\{S_k-U_k<x\}\cap \{S_k \ge x \}) \\ &= P(x\le S_k \le x +U_k ) \\ &= \int_0^1 \left( \int_{x}^{\min\{x+u,k\}} f(s;k)ds\right)du \\ \end{align}

And the expectation $E(n(x))$ is then calculated as

$$E(n(x)) = \sum_{k=1}^{+\infty}\left(\int_0^1 \int_{x}^{\min\{x+u,k\}} f(s;k)dsdu\right)$$

PS: I think the solution of leonbloy is better than mine.

Answer 2

You seem on the right track.

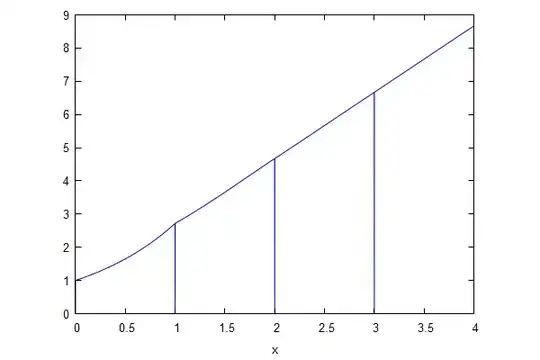
Letting $g(x) = E[n(x)]$, applying the total law of expectation and using the fact that $f_U(u)=1 [0\le u \le 1]$ I get:

$$ g(x) =\begin{cases} 1 + \int_0^x g(u) du &0\le x\le1\\ 1 + \int_{x-1}^x g(u) du & x >1 \\ \end{cases} $$

This gives $g(x) = \exp(x)$ for $0\le x\le1$

In general, $g(x)$ can be expressed as a sum of piecewise differentiable functions in each interval $[k,k+1]$, $g(x) = \sum_{k=0}^\infty g_k(x) $ where

$$g_k(x)= \exp(x-k) h_k(x-n) \quad [ k\le x < k+1] $$ and $h_k(\cdot)$ is a polynomial of degree $k$

The first values are $h_0(x)=1$, $h_1(x)=e-x$ , $h_2(x)=\frac{{{x}^{2}}}{2}-e x+{{e}^{2}}- e$

For large $x$, $g(x) \approx 2x + \frac23$ (empirically)

Added: The functions $h_k(x)$ are produced by this recursion:

$$ h_k(x) = e \,h_{k-1}(1) - \int_0^x h_{k-1}(u) du $$