4

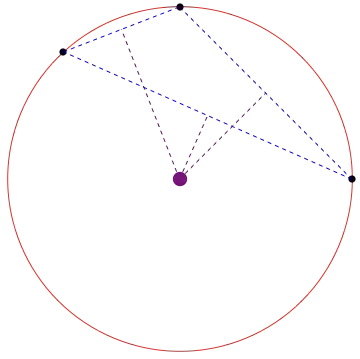
In learning about the general formula for a circle: $$(x-h)^2 + (y-k)^2 = r^2$$ my book states that $3$ points are sufficient to guarantee the solution (or absence of solution) for an unique circle.

It follows this up by explaining that $3$ different points creates $3$ different equations...namely:

1) $(x_1-h)^2 + (y_1-k)^2 = r^2\;$ where $\;(x_1,y_1)\;$ is the first point provided
2) $(x_2-h)^2 + (y_2-k)^2 = r^2\;$ where $\;(x_2,y_2)\;$ is the second point provided
3) $(x_3-h)^2 + (y_3-k)^2 = r^2\;$ where $\;(x_3,y_3)\;$ is the third point provided

I'm okay with this as I'm familiar with the whole "$3$ equations for $3$ unknowns".

However, the book's explanation concludes with the statement:

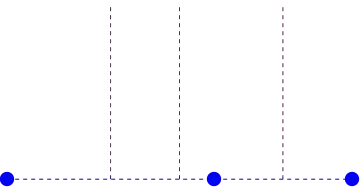
"The equations can't be linearly dependent since the points that lead to them are all different". I am not particularly familiar with linear algebra so I do not understand the significance of this statement. Is there a visual representation of this statement that can help me understand what they mean?

S.C.
  • 4,984
  • 2
    as long as you have three points A,B,C that are distinct and not collinear, draw the perpendicular bisector of the line segment AB, then draw the perpendicular bisector of the line segment BC, these two constructed lines meet in the correct center. In fact, if you also draw the perpendicular bisector of the line segment CA, all three lines meet in the correct center. – Will Jagy Jan 05 '19 at 22:25
  • That is interesting. Could you explain to me why that is the case? Is that a visual demonstration of what it means to be linearly independent? Or is that just a coincidental phenomenon that you observe with circles defined by 3 unique points. – S.C. Jan 05 '19 at 22:30
  • 1
    meanwhile, given coordinates for the three points, it is not hard to find equations for the three lines. – Will Jagy Jan 05 '19 at 22:30
  • 1
    If we call the center P, we know that PAB is an isosceles triangle, as P must be the same distance from A and B. Before we are quite sure where P is, we still know it lies on the perpendicular bisector of segment AB, as the altitude of an isosceles triangle also bisects the opposing side. I am ignoring the linear algebra concepts – Will Jagy Jan 05 '19 at 22:33
  • The linear algebra concepts are what I am interested in haha. – S.C. Jan 05 '19 at 22:35
  • 2
    Understood. I really recommend you draw some pictures my way before pushing on with the system of equations; the bisector method goes back about two thousand years and is easy. Also, in your question above, it should read $y_1- k$ and $y_2-k$ and $y_3-k$ – Will Jagy Jan 05 '19 at 22:38

3 Answers3

4

Sometimes a few figures are worth a thousand words:

enter image description here

enter image description here

Top: Three non-collinear points determine a triangle, each leg of which will be a chord of the circle. A perpendicular to each chord must go through the center of the circumscribed circle.

Bottom: If the three points are collinear, then perpendiculars to their three defined segments are parallel, thus never meet, thus cannot define a circle.

Clear?

David G. Stork
  • 29,774
  • I assume the lower image is when you collapse the shorter 2 legs of the triangle onto the longest leg of the triangle? (and the resulting vertical lines in the lower image are where the bisecting lines in the upper image would land) What is the significance of "collapsing two lines on to one line" ... i.e. why did you choose to emphasize this? – S.C. Jan 06 '19 at 00:09
  • When the three (blue) points are linearly dependent (i.e., you can obtain one of the points by a linear combination of the two others), the points fall on a line (hence "linear") and the bisecting perpendiculars which intersect at the center of the generated circle, instead do not intersect... hence no circle... hence no solution. – David G. Stork Jan 06 '19 at 00:13
  • I guess my confusion is that I do not understand how, given two points that lay on a circle, I could actually create a linearly DEPENDENT point derived from those two points. – S.C. Jan 06 '19 at 00:19
  • Illuminating, but not quite apropos. The claim in questions is that the three circle equations in $h$ and $k$ are linearly independent iff the three points are distinct. We haven’t yet gotten to whether or not that system of three independent equations has a solution. – amd Jan 06 '19 at 00:19
2

The pictures in @DavidGStork 's lovely answer explain why the three equations produce a unique solution.

I want to add a discussion of the algebra, and a possible correction.

When the author writes

The equations can't be linearly dependent since the points that lead to them are all different

the intent is to tell you that you can't deduce the third equation from the first two. That means you really do have three independent conditions on the three unknowns, which is usually what you need to guarantee a solution.

However

  • The simple assertion that the "points are different" does not in itself prove the independence. For that you need an argument like the one in the picture.

  • As written, these are not linear equations. The variables $h$ and $k$ appear squared. So they should be described as independent, but not linearly independent. With a little algebra you can combine them in pairs to produce two linear equations for $h$ and $k$. Those you can solve using what you learn in high school algebra. Finding where two lines cross by solving two equations in two unknowns is the only "linear algebra" you need. Then you can use any one of the three equations to find $r^2$, so $r$.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
1

This doesn’t have to do with linear algebra per se, although the idea of linear independence is central to that discipline. To state the claim differently, none of the three equations is redundant—none of them can be obtained by adding multiples of the other two to each other—because the three points are distinct.

Assume that the equations are dependent. W.l.o.g. we’ll say that it’s the third one that’s a linear combination of the other two. Since its right-hand side must be $r^2$, there’s some real number $\lambda$ for which the coefficients of the left-hand side of $$(1-\lambda)((x_1-h)^2+(y_1-k)^2)+\lambda((x_2-h)^2+(y_2-k)^2) = r^2 \tag{*}$$ are equal to those in the left-hand side of the original third equation. Now, that equation represents a circle with radius $r$ centered at $(x_3,y_3)$. With a bit of work, equation (*) can be rearranged into $$(h-((1-\lambda)x_1+\lambda x_2))^2 + (k-((1-\lambda)y_1+\lambda y_2))^2=r^2-\lambda(1-\lambda)((x_1-x_2)^2+(y_1-y_2)^2).$$ This is an equation of a circle with center at $(1-\lambda)(x_1,y_1)+\lambda(x_2,y_2)$, which lies somewhere on the line through $(x_1,y_1)$ and $(x_2,y_2)$. For its radius to be $r$, the second term on the right must vanish. This can occur in three ways: either $(x_1,y_1)=(x_2,y_2)$; $\lambda = 0$, in which case $(x_3,y_3)=(x_1,y_1)$; or $\lambda=1$, in which case $(x_3,y_3)=(x_2,y_2)$. By hypothesis, the three points are distinct, so the three equations must be linearly independent.

amd
  • 53,693
  • I can add a picture if you like, but the basic idea is that combining the first two equations gives you a family of circles of varying radii, but the only two members of that family that have the required radius are the two circles that generated it. – amd Jan 06 '19 at 00:49