0

The following formula shall be proved by induction: $$F(m+n) = F(m-1) \cdot F(n) + F(m) \cdot F(n+1)$$ Where $F(i), i \in \mathbb{N}_0$ is the Fibonacci sequence defined as: $F(0) = 0$, $F(1) = 1$ amd $$F(n+1) = F(n) + F(n-1) \text{ for } n \geq 1.$$

How would you go about this task, especially considering that you have two variables which may be changed? Do you have to look at three cases ($m$ increases, $n$ increases, both $m$ and $n$ increase) in order to fully prove it or is there an easier way?

Robert Z
  • 145,942
StckXchnge-nub12
  • 541

4 Answers4

5

Here is a proof in the same spirit as RobertZ's.

First, let's relate the Fibonacci numbers to the following problem:

Suppose that you want to go up some flight of stairs and at every step you can take either one or two stairs: in how many ways can you get up the stairs?

Well, if we say that there are $n$ stairs, then it turns out there are $F_{n+1}$ ways to do it.

A very easy inductive proof shows why:

Base cases: If there is $1$ stairs, you can do it in only $1$ way, and indeed $F_{1+1}=F_2=1$. If there are $2$ stairs, then there are two ways: either take two steps of $1$, or take one step of $2$. And indeed, $F_{2+1}=F_3=2$

Inductive step: Say you have $n >2$ stairs. For your first step you can either go one up or two stairs up. By inductive hypothesis, there are $F_{n}$ ways to finish climbing the $n-1$ stairs after having taken a step of $1$ stairs, and there are $F_{n-1}$ ways to finish climbing the $n-2$ stairs after having taken a step of $2$ stairs. So, there are $F_{n}+F_{n-1}=F_{n+1}$ ways to climb $n$ stairs.

OK, so now that we have made a connection between the Fibonacci numbers and the number of ways to climb stairs in this way, we can prove your desired result very quickly:

Let's climb $m+n-1$ stairs. We now know we can do this in $F_{m+n}$ ways. But note that there are two different possibilities for us climbing those $m+n-1$ stairs:

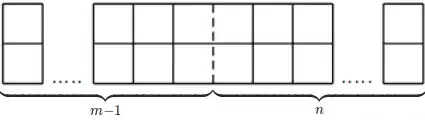
  1. The first way is that as we climb the stairs, we will at some point have climbed exactly $n$ stairs. If this happens, then there are $m-1$ stairs left to climb, which can be done in $F_m$ ways. And since then there are $F_{n+1}$ ways to climb the first $n$ stairs, that means that there are $F_m \cdot F_{n+1}$ ways to climb all the $m+n-1$ stairs this way.

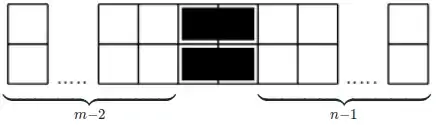
  2. The second way is that at some point we will have climbed exactly $n-1$ stairs, which can be done in $F_{n}$ ways, after which we take a single step of $2$ stairs, and then finish climbing the remaining $m-2$ stairs. This can therefore be done in $F_{m-1} \cdot F_{n}$ ways

The total number of ways to climb the $m+n-1$ stairs, then, is the sum of these two ways, and so it must be true that:

$$F_{m+n} = F_{m-1} \cdot F_{n} + F_{m} \cdot F_{n+1}$$

So note that after I established the connection between climbing stairs and the Fobonacci numbers, the proof was straightforward (and did not use induction). But to establish the connection, I used induction.

Bram28
  • 100,612
  • 6
  • 70
  • 118
  • Nice variant (+1). See also https://math.stackexchange.com/a/11527/299698 – Robert Z Dec 31 '18 at 20:53
  • @RobertZ :) And here I thought I was original ... – Bram28 Jan 01 '19 at 13:25
  • Have you any suggestion to improve my answer? Unfortunately it did not have much success :-( – Robert Z Jan 01 '19 at 13:34
  • @RobertZ Maybe you could try and show a picture of the domino covering ... both to establish the connection between F numbers and dominoes and then applied to this particular problem – Bram28 Jan 01 '19 at 13:54
3

You can get away with inducting on just $n$:

$$ \begin{align} F(m + n) & = F(m + (n - 1)) + F(m + (n -2))\\ & = F(m-1)F(n-1) + F(m)F(n) + F(m-1)F(n-2) + F(m)F(n-1) \\ & = F(m-1)[F(n-1) + F(n-2)] + F(m)[F(n)+F(n-1)] \\ & = F(m-1)F(n) + F(m)F(n+1)\end{align}$$

ODF
  • 1,590
  • Can you explain in greater detail the steps you took? You already lost me on the very first one. It seems you have somehow replaced $F(n)$ with the recursive definition of the fibonacci sequence (the last formula I listed), but I didn't even know you can split apart the term partially like that. Isn't the $F(m+n)$ to be seen as static, i.e. if $m=2$ and $n = 3$, you have to solve the entire sum $F(5)$, and can't just partially solve the "3 part" of the fibonacci? Hard to explain my issue, I hope you get what I mean. – StckXchnge-nub12 Dec 31 '18 at 17:42
  • Hi, using your example: if $m = 2, n = 3$, $n + m = 5$ then $F(5) = F(4) + F(3)$ by the definition of the Fibonacci sequence. Note then that $n + m -1 = 4$ and $n + m - 2 = 3$ which is my first step. – ODF Dec 31 '18 at 17:46
  • In the second step I induct on $n$, in the third I just gather like terms and in the final I use the fact that $F(n) = F(n-1) + F(n-2)$ and that $F(n+1) = F(n) + F(n-1)$. – ODF Dec 31 '18 at 17:47
  • Alright, I've finally understood your solution; thank you! Just for the record, in order to turn it into an actual proof by induction, I believe you have to proof $F(m+n+1) = F(m-1)\cdot F(n+1) + F(m) \cdot F(n+2)$ using the very same steps you took. – StckXchnge-nub12 Dec 31 '18 at 18:28
  • I must revise myself. I think there's an issue here. In the second line, you would apply the induction precondition. If we are inducting on $n$, that means we can only apply it on an $n$, but not e.g. on an $n-1$. But in your calculations you do apply it on just any $n$, so you basically assume that the precondition already applies for every single $n$ (i.e. $n, n+1, n-1, \ldots$) when in reality we only defined it to apply to a fix $n$ for the sake of the proof. – StckXchnge-nub12 Dec 31 '18 at 19:59
  • To prove it's true for $n$, I assume it's true for any $k<n$. Note that I've only applied induction on $n-1$ and $n-2$, which are both strictly less than $n$, so this is all ok. – ODF Jan 01 '19 at 12:37
1

A combinatorial proof (no induction).

Using the representation of the Fibonacci numbers as the numbers of domino coverings the given identity can be shown in a quick and elegant way.

It is known that the number of domino coverings of a $2\times N$ grid is $F_{N+1}$. Consider the number of domino coverings of a $2\times (m+n-1)$ grid. Any covering can be of two types.

1) The covering has a pair of horizontal dominoes at position $m-1$ and $m$. enter image description here

Therefore on the left side we have a covering of a $2\times (m-2)$ grid and on the right side we have a covering of a $2\times (n-1)$ grid. Therefore the number of such coverings is $F_{m-1}\cdot F_{n}$.

2) The covering can be split into two coverings, one of a $2\times (m-1)$ grid and another of a $2\times n$ grid. enter image description here

Therefore the number of such coverings is $F_{m}\cdot F_{n+1}$.

Finally we may conclude that the number of domino coverings of a $2\times (m+n-1)$ grid is $$F_{m+n}=F_{m-1}\cdot F_{n}+F_{m}\cdot F_{n+1}.$$

Robert Z
  • 145,942
1

I won't mention every use of induction. Define $$M:=\left(\begin{array}{cc} 0 & 1\\ 1 & 1 \end{array}\right),\,V_{n}:=\left(\begin{array}{c} F_{n}\\ F_{n+1} \end{array}\right)=M^{n}\left(\begin{array}{c} 0\\ 1 \end{array}\right)$$ so $M^{m}=\left(\begin{array}{cc} F_{m-1} & F_{m}\\ F_{m} & F_{m+1} \end{array}\right)$ and $$\left(\begin{array}{c} F_{m+n}\\ F_{m+n+1} \end{array}\right)=M^{m}\left(\begin{array}{c} F_{n}\\ F_{n+1} \end{array}\right)=\left(\begin{array}{c} F_{m-1}F_{n}+F_{m}F_{n+1}\\ F_{m}F_{n}+F_{m+1}F_{n+1} \end{array}\right).$$

J.G.
  • 115,835