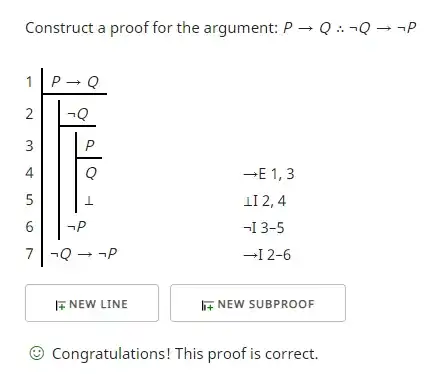
I'm asked to give a formal proof of $(p → q) → (¬q → ¬p)$ using natural deduction. Is that like saying prove $⊢ (p → q) → (¬q → ¬p$), where it should be proved from nothing?
Asked
Active
Viewed 715 times
1
-
1Exactly; you have to start assuming one or more premises that you will discharge later. – Mauro ALLEGRANZA Dec 29 '18 at 13:13
-
1Please use MathJax in future. – Shaun Dec 29 '18 at 13:18
-
Assume $q$ follows from $p$. Further assume not $q$. What can you say about $p$? By the way, this is called the contrapositive. – David Diaz Dec 29 '18 at 14:11
-
Not a duplicate, but the only answer to this question solves 95% of this problem. – Git Gud Dec 29 '18 at 14:23
-
What rules do you have to work with? There are many different systems of 'natural deduction', each with their own set of rules. – Bram28 Dec 29 '18 at 18:13
2 Answers
1
The following proof uses modus tollens (MT):
However, one can derive the modus tollens rule in the following way. This uses the proof provided on page 138 of forallx linked to below along with a link to the proof checker used here:
Kevin Klement's JavaScript/PHP Fitch-style natural deduction proof editor and checker http://proofs.openlogicproject.org/
P. D. Magnus, Tim Button with additions by J. Robert Loftis remixed and revised by Aaron Thomas-Bolduc, Richard Zach, forallx Calgary Remix: An Introduction to Formal Logic, Winter 2018. http://forallx.openlogicproject.org/
Frank Hubeny
- 1,527
0
Hint: the following statements are all equivalent:
- $p\to q$
- $\neg p\lor q$
- $\neg\neg q\lor\neg p$
- $\neg q\to\neg p$
J.G.
- 115,835
-
2The formal proof that comes naturally to me uses none of this. How is this helpful? – Git Gud Dec 29 '18 at 14:20
-
@GitGud If you have a different route, well done. But to any future reader considering this problem who doesn't, the use comes in providing a sequence of statements worth proving equivalent. How you stitch them together into a proof depends on your preferred notation. – J.G. Dec 29 '18 at 15:59
-
I didn't say what I should have said. How do you go from this to a formal proof? As I see it, you need to go to the moon and back, I don't see how this can be helpful. – Git Gud Dec 29 '18 at 16:09