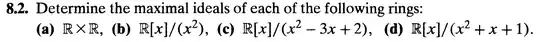Determine the maximal ideals of $\mathbb R^2$ by determining **all** its ideals.

Question

This is a letter of an exericse in Artin Algebra and has been asked and answered here as well as by Brian Bi here and Takumi Murayama here. I had a different approach here and have yet another approach.

$\mathbb R$ is a field so its only ideals are $(1)$ and $(0)$. Thus, by Structure of ideals in the product of two rings all the ideals of $\mathbb R^2$ are $$(0)\times(0),(1)\times(1),(0)\times(1),(1)\times(0)$$. Then it's obvious $$(0)\times(1),(1)\times(0)$$ are the maximal ideals.

Is this correct also?

Answer 1

Yes, since $(1) \times (1) = \mathbb{R} \times \mathbb{R}$ is the whole ring and $(0) \times (0)$ is contained in both $(0) \times (1)$ and $(1) \times (0)$. It is also clear that $(0) \times (1) \not \subset (1) \times (0)$ and vice versa.