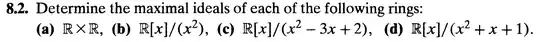This is a letter of an exericse in Artin Algebra and has been asked and answered here as well as by Brian Bi here and Takumi Murayama here. I have a different approach.
An earlier exercise is to prove $\mathbb R^2 \cong \mathbb R[x]/(x^2-1)$. One way to do that is with the surjective homomorphism $\varphi:\mathbb R[x] \to \mathbb R^2$ defined by $\varphi(x)=(1,-1)$. This solution is in the answer here and in the answer by Takumi Murayama.
The maximal ideals in $\mathbb R[x]/(x^2-1)$ include the principal ideals $([x-1+(x^2-1)])$ and $([x+1+(x^2-1)])$.
The corresponding maximal ideals in $\mathbb R^2$ are principal ideals generated by
$$\overline\varphi([x-1+(x^2-1)])=(\overline\varphi \circ \pi) (x-1) = \varphi(x-1)=(0,-2)$$
and
$$\overline\varphi([x+1+(x^2-1)])=(\overline\varphi \circ \pi) (x+1) = \varphi(x+1)=(2,0)$$
where $\overline \varphi$ is the isomorphism from $R[x]/(x^2-1) \to \mathbb R^2$.
The principal ideal generated by $(0,\pm 2)$ is the same as the one generated by $(0,1)$. Also, the one by $(\pm 2,0)$ is the same as the one by $(1,0)$.
We know that $((0,1))=0\times \mathbb R, ((1,0))=\mathbb R \times 0$.
After proving that $([x-1+(x^2-1)])$ and $([x+1+(x^2-1)])$ are the only maximal ideals in the quotient ring, we can say $((0,1))=0\times \mathbb R, ((1,0))=\mathbb R \times 0$ are the only maximal ideals in $\mathbb R^2$.
Is this correct?
To recap, I answered the maximal ideals of $\mathbb R[x]/(x^2-1)$ instead of for $\mathbb R^2$. Then I converted the ideals from $\mathbb R[x]/(x^2-1)$ to $\mathbb R^2$.