How to prove that Fibonacci number pairs are the only solution to this equation?

Question

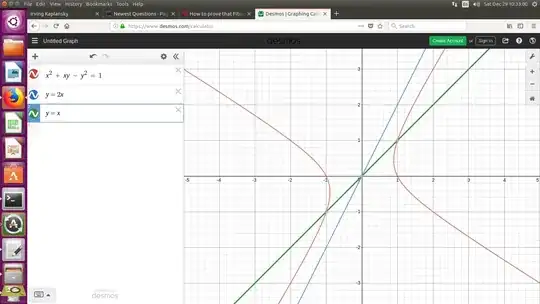
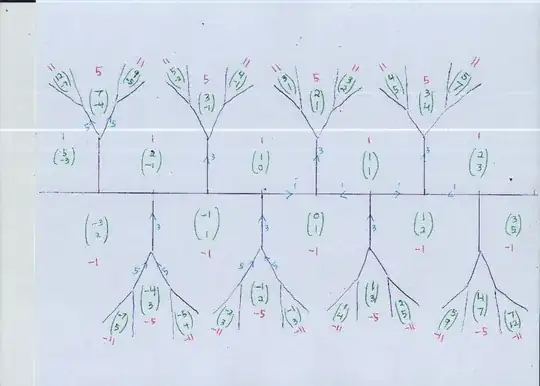
I need to find all the solutions to the equation

$$x^2 + xy - y^2 = 1$$

However, I am not interested in using Pell's equation the way it has been suggested in a similar question here: Find all positive inegers solution for $x^2-xy-y^2=1$

Rather, my book gives a few observations and I exploit them to find the solutions. The following were the observations the book gave:

If $x$ and $y$ are solutions then $(x+y,x+2y)$ and $(2x-y,-x+y)$ are also solutions

and

$x \leq y < 2x$

I am interested in finding only positive integer solutions. After playing around a little with the two points, first point in particular, I ended up with solutions of the form $(F_{2n-1},F_{2n})$. However I am unable to prove that these are the only positive integer solutions possible for the given equation. I feel that the proof will run quite similar to that of Pell's equation and will make use of the second point but I am unable to prove it. Any help please!!

Answer 1

I can recommend Weissman for the Conway topograph. Domain topograph page 233, automorphisms page 240, range topograph page 244, the river is periodic page 286. I'm not seeing an explicit statement that the "automorphism" generator can be seen if we draw the "domain" and "range" topographs together, as I do. Implicit, certainly. Note: I had not noticed that Weissman writes the "domain" vectors as rows. I have always drawn them as columns. So, my automorphism matrix is two columns side by side.

The attitude of Hurwitz (1907) is what they are trying to get across. A solution $(x,y)$ with $x,y > 0$ and $x^2 + xy - y^2 =1$ will be called "fundamental" if the backwards move $$ (x,y) \mapsto (2x-y, -x+y) $$ leads to one or both elements negative or zero: either $$ 2x-y \leq 0 \; \; \mbox{OR} \; \; -x+y \leq 0 $$ As this diagram shows, we never get $y \geq 2 x$ on the hyperbola part within the first quadrant. We do get $y \leq x,$ namely the solution $(1,1)$ is moved "backwards" to $(1,0)$ The simple result is that all positive solutions are found by beginning with $(1,1)$ and repeatedly moving forwards to $$ (x,y) \mapsto (x+y, x+2y) $$ This mapping is the generator of the (oriented) automorphism group of the quadratic form. The generator can be seen in my diagrams of the Conway Topograph method (columns in green in the later diagram).

The matrix is $$ A = \left( \begin{array}{rr} 1&1\\ 1&2 \end{array} \right) $$ Cayley-Hamilton tells us, from $A^2 - 3A + I + 0$ or $A^2 = 3 A - I\; , \;$ that $$ x_{n+2} = 3 x_{n+1} - x_n, $$ $$ y_{n+2} = 3 y_{n+1} - y_n. $$

If you don't know Cayley-Hamilton, just solve: $$ x_{n+2} = x_{n+1} + y_{n+1} = (x_n+y_n) + (x_n + 2 y_n) \; , \; $$ $$ x_{n+2} = 2 x_n + 3 y_n \; , \; $$ $$ 3 x_{n+1} = 3 x_n + 3 y_n \; , \; $$ $$ x_{n+2} - 3 x_{n+1} = - x_n \; . \; $$