Does anyone know how to calculate the volume of an irregular octahedron from the lengths of the edges?
The octahedron has triangular faces, but the only information are the edge lengths.
Alternatively, how might I calculate the length of a line drawn ( the yellow dashed line) between two opposing vertices? If this known it can be split into 4 irregular tetrahedra.
In the Image the different edge lengths are coour coded, i.e all green edges are length x, blue edges are length y...
Let $w$, $x$, $y$, $z$ be the edge lengths, and let $d$ be a body diagonal. Then $s:=d^2$ satisfies this quartic (barring typos):
$$\begin{align} 0 &= s^4 (-w + x + y + z) (w - x + y + z) (w + x - y + z)(w + x + y - z) \\[4pt] &- 12 s^3 (w x + y z)(w y + x z)(wz+x y) \\[4pt] &+2 s^2 \left(\begin{array}{c} \sigma_1^4 \sigma_2^2 - 4 \sigma_1^2 \sigma_2^3 - 2 \sigma_1^5 \sigma_3 + 8 \sigma_1^3 \sigma_2 \sigma_3 \\ + 8 \sigma_1 \sigma_2^2 \sigma_3 - 10 \sigma_1^2 \sigma_3^2 - 12 \sigma_2 \sigma_3^2 + 8 \sigma_1^4 \sigma_4 \\ - 44 \sigma_1^2 \sigma_2 \sigma_4 + 32 \sigma_2^2 \sigma_4 + 48 \sigma_1 \sigma_3 \sigma_4 - 32 \sigma_4^2 \end{array}\right) \\[4pt] &-4 s (w x + y z)(w y + zx)(wz+xy) \left( \begin{array}{c} 2 \sigma_1^4 - 8 \sigma_1^2 \sigma_2 + 3 \sigma_2^2 + 10 \sigma_1 \sigma_3 - 8 \sigma_4 \end{array}\right) \\[4pt] &-\left(\begin{array}{c} \sigma_1^4 \sigma_2^4 - 4 \sigma_1^2 \sigma_2^5 - 4 \sigma_1^5 \sigma_2^2 \sigma_3 + 16 \sigma_1^3 \sigma_2^3 \sigma_3 \\ + 8 \sigma_1 \sigma_2^4 \sigma_3 + 8 \sigma_1^4 \sigma_2 \sigma_3^2 - 64 \sigma_1^2 \sigma_2^2 \sigma_3^2 + 64 \sigma_1 \sigma_2 \sigma_3^3 \\ - 12 \sigma_3^4 + 8 \sigma_1^6 \sigma_2 \sigma_4 - 48 \sigma_1^4 \sigma_2^2 \sigma_4 + 64 \sigma_1^2 \sigma_2^3 \sigma_4 \\ - 16 \sigma_2^4 \sigma_4 + 64 \sigma_1^3 \sigma_2 \sigma_3 \sigma_4 - 64 \sigma_1 \sigma_2^2 \sigma_3 \sigma_4 - 24 \sigma_1^2 \sigma_3^2 \sigma_4 \\ - 32 \sigma_2 \sigma_3^2 \sigma_4 - 12 \sigma_1^4 \sigma_4^2 - 32 \sigma_1^2 \sigma_2 \sigma_4^2 + 64 \sigma_2^2 \sigma_4^2 \end{array}\right) \end{align} \tag{$\star$}$$ where the $\sigma_i$ are the symmetric polynomials $$\sigma_1 := w + x + y + z \qquad \sigma_2 := w x + w y + w z + x y + x z + y z$$ $$\sigma_3 := w x y + w x z + w y z + x y z \qquad \sigma_4 := w x y z$$
As a sanity check, when $w=x=y=z$ (ie, the octahedron is regular), equation $(\star)$ reduces to $$16 s w^4 (s-2 w^2)^3 = 0$$ with root $s = 2 w^2$ corresponding to $d = w \sqrt{2}$, as expected.
The discriminant of $(\star)$ is
$$\begin{align}\Delta = 4096&\cdot(w^2 - x^2)^2 (w^2 - y^2)^2 (w^2-z^2)^2 (x^2 - y^2)^2 (x^2-z^2)^2 (y^2 - z^2)^2 \\ &\cdot (w^2 - x^2 + y^2 - z^2 - w y - z x )^2 (w^2 - x^2 + y^2 - z^2 + w y + z x )^2 \\ &\cdot (w^2 + x^2 - y^2 - z^2 - w x - y z )^2 (w^2 + x^2 - y^2 - z^2 + w x + y z )^2 \\ &\cdot (w^2 - x^2 - y^2 + z^2 - w z - x y )^2 (w^2 - x^2 - y^2 + z^2 + w z + x y )^2 \end{align}$$
If $\Delta = 0$ (that is, when at least two edge-lengths match, or at least one of those other factors vanishes), then the polynomial has a multiple root. Otherwise, the polynomial has either four real, or else four non-real, roots; Descartes' Rule of Signs, and/or or the techniques described here could potentially help refine our understanding of the nature of the roots, but the coefficients are sufficiently complicated that a general sign analysis is difficult.
In the all-real-roots case, due to symbolic symmetry, the roots must correspond to the (squares of the) three "body diagonals" of the octahedron, and a spare. (Perhaps the last root is negative, and cannot be the square of a diagonal.)
As for volume ... The complicated nature of the diagonal length doesn't inspire a great deal of hope for a nice answer. Nevertheless, I'm still crunching some symbols in Mathematica, and will update this answer later.
... well, it's later ...
So far, finding a polynomial involving volume and side-lengths has proven difficult. Intervening formulas are simply enormous (with $(\star)$ being svelte by comparison). With no final result to show, I'll give some formulas that may help others.
We can think of the solid as four tetrahedra joined along the yellow diagonal, $d$. Writing $V_w$ for the volume of the tetrahedron with an equilateral $w$-colored face, the Cayley-Menger determinant tells us that
$$\begin{align} 144\,V_w^2 &= w^2 \left(\; -w^4 - y^4 - z^4 - d^4 + w^2 y^2 + w^2 z^2 + w^2 d^2 + y^2 z^2 + y^2 d^2 + z^2 d^2\;\right) \\ 144\,V_x^2 &= x^2 \left(\; - x^4 - y^4 - z^4 - d^4 + x^2 y^2 + x^2 z^2 + x^2 d^2 + y^2 z^2 + y^2 d^2 + z^2 d^2 \;\right) \\ 144\,V_y^2 &= y^2 \left(\; -y^4-w^2-x^4-d^4 + y^2 w^2 + y^2 x^2 + y^2 d^2 + w^2 x^2 + w^2 d^2 + x^2 d^2 \;\right) \\ 144\,V_z^2 &= z^2 \left(\; -z^4-w^2-x^4-d^4 + z^2 w^2 + z^2 x^2 + z^2 d^2 + w^2 x^2 + w^2 d^2 + x^2 d^2 \;\right) \\ \end{align}$$ where I have taken the $w$- and $x$-colored equilaterals to share the vertex at one end of $d$, and the $y$- and $z$-colored equilaterals to share the vertex at the other end of $d$.
The octahedral volume ($V$) is, of course, the sum of these tetrahedral volumes, but the square roots prevent combination. Through a process of repeated squarings (or iterations of Mathematica's Resultant function), one gets a polynomial with $V$ and even powers of the $V_{-}$s:
$$\begin{align} 0 &= V^{16} \\ &- 8 V^{14} \sigma_1 \\ &+ 4 V^{12}\left(7\sigma_1^2-4\sigma_2\right) \\ &- 8 V^{10} \left(7 \sigma_1^3 - 12 \sigma_1 \sigma_2 + 16 \sigma_3 \right) \\ &+2 V^8 \left(35 \sigma_1^4 - 120 \sigma_1^2 \sigma_2 + 48 \sigma_2^2 + 256 \sigma_1 \sigma_3 - 1088 \sigma_4\right) \\ &-8 V^6 \left(7 \sigma_1^5 - 40 \sigma_1^3 \sigma_2 + 48 \sigma_1 \sigma_2^2 + 96 \sigma_1^2 \sigma_3 - 128 \sigma_2 \sigma_3 - 320 \sigma_1 \sigma_4\right) \\ &+4 V^4 \left(\begin{array}{c} 7 \sigma_1^6 - 60 \sigma_1^4 \sigma_2 + 144 \sigma_1^2 \sigma_2^2 - 64 \sigma_2^3 + 128 \sigma_1^3 \sigma_3 \\ - 512 \sigma_1 \sigma_2 \sigma_3 + 1024 \sigma_3^2 + 320 \sigma_1^2 \sigma_4 - 1792 \sigma_2 \sigma_4 \end{array}\right) \\ &-8 V^2 \left(\begin{array}{c}\sigma_1^7 - 12 \sigma_1^5 \sigma_2 + 48 \sigma_1^3 \sigma_2^2 - 64 \sigma_1 \sigma_2^3 + 16 \sigma_1^4 \sigma_3 \\ - 128 \sigma_1^2 \sigma_2 \sigma_3 + 256 \sigma_2^2 \sigma_3 + 192 \sigma_1^3 \sigma_4 - 768 \sigma_1 \sigma_2 \sigma_4 + 1024 \sigma_3 \sigma_4\end{array}\right) \\ &+\left(\sigma_1^4 - 8 \sigma_1^2 \sigma_2 + 16 \sigma_2^2 - 64 \sigma_4\right)^2 \end{align} \tag{$\star\star$}$$
Here, the $\sigma_i$ are also symmetric polynomials, but in the squares of tetrahedral volumes:
$$\sigma_1 := V_w^2 + V_x^2 + V_y^2 + V_z^2 \qquad \sigma_2 := V_w^2 V_x^2 + V_w^2 V_y^2 + V_w^2 V_z^2 + V_x^2 V_y^2 + V_x^2 V_z^2 + V_y^2 V_z^2$$ $$\sigma_3 := V_w^2 V_x^2 V_y^2 + V_w^2 V_x^2 V_z^2 + V_w^2 V_y^2 V_z^2 + V_x^2 V_y^2 V_z^2 \qquad \sigma_4 := V_w^2 V_x^2 V_y^2 V_z^2$$
That's all well and good, I suppose, but recall that $(\star\star)$ involves the diagonal length $d$. A full solution to the problem posed would require eliminating $d$ from $(\star\star)$, using $(\star)$. Although it's just a matter of hitting the equations once more with Resultant, the operation on polynomials this degree and size is quite computationally expensive. I've let my laptop chug away at the problem for a good while without completion; I may try again later.
Let $P_1,\ldots,P_6$ denote the vertices of the octahedron, with $P_i$ being opposite $P_j$ if and only if $i+j=7$. In here, indices $i,j,\ldots$ are always from $\{1,2,\ldots,6\}$.
Let $D_{ij} = D_{ji}$ be the squared euclidean distance between $P_i$ and $P_j$. We know $D_{ij}$ unless $i+j=7$. Thus exactly three $D_{ij}$ with $i<j$ are unknown.
Suppose for a moment that we had the vertices given in cartesian coordinates: $P_i = (x_i, y_i, z_i)$. Then a formula for the oriented octahedron's volume $V$ would be
$$ 6V = \begin{vmatrix} 1 & 0 & 0 & x_1 & y_1 & z_1 \\ 0 & 1 & 0 & x_2 & y_2 & z_2 \\ 0 & 0 & 1 & x_3 & y_3 & z_3 \\ 0 & 0 & 1 & x_4 & y_4 & z_4 \\ 0 & 1 & 0 & x_5 & y_5 & z_5 \\ 1 & 0 & 0 & x_6 & y_6 & z_6 \end{vmatrix} = \begin{vmatrix} (x_4 - x_3) && (y_4 - y_3) && (z_4 - z_3) \\ (x_5 - x_2) && (y_5 - y_2) && (z_5 - z_2) \\ (x_6 - x_1) && (y_6 - y_1) && (z_6 - z_1) \end{vmatrix}$$
In other words, the octahedron's volume is $1/6$ of the volume of the parallelepiped spanned by its diagonal vectors.
Squaring the above equation and using multiplicativity of determinants, we get
$$\begin{align} 288\,V^2 &= \det\left(\left(2\langle P_{7-i}-P_i, P_{7-j}-P_j\rangle\right)\right)_{i,j=1,\ldots,3} \\ &= \det\left(\left(D_{i,7-j}-D_{i,j}+D_{7-i,j}-D_{7-i,7-j}\right)\right)_{i,j=1,\ldots,3} \\ &= \begin{vmatrix} 2\color{red}{D_{16}} & (D_{15}-D_{12}+D_{62}-D_{65}) & (D_{14}-D_{13}+D_{63}-D_{64}) \\ (D_{26}-D_{21}+D_{51}-D_{56}) & 2\color{red}{D_{25}} & (D_{24}-D_{23}+D_{53}-D_{54}) \\ (D_{36}-D_{31}+D_{41}-D_{46}) & (D_{35}-D_{32}+D_{42}-D_{45}) & 2\color{red}{D_{34}} \end{vmatrix} \end{align}$$
with unknowns displayed in red. A Cayley-Menger-like version of the above formula is
$$288\,V^2 = \begin{vmatrix} 0 &0 &0 &1 &0 &0 &0 &0 &1 \\ 0 &0 &0 &0 &1 &0 &0 &1 &0 \\ 0 &0 &0 &\color{blue}1 &\color{blue}1 &1 &1 &\color{blue}1 &\color{blue}1 \\ 1 &0 &\color{blue}1 &0 &D_{12} &D_{13} &D_{14} &D_{15} &\color{red}{D_{16}} \\ 0 &1 &\color{blue}1 &D_{21} &0 &D_{23} &D_{24} &\color{red}{D_{25}} &D_{26} \\ 0 &0 &1 &D_{31} &D_{32} &0 &\color{red}{D_{34}} &D_{35} &D_{36} \\ 0 &0 &1 &D_{41} &D_{42} &\color{red}{D_{43}} &0 &D_{45} &D_{46} \\ 0 &1 &\color{blue}1 &D_{51} &\color{red}{D_{52}} &D_{53} &D_{54} &0 &D_{56} \\ 1 &0 &\color{blue}1 &\color{red}{D_{61}} &D_{62} &D_{63} &D_{64} &D_{65} &0 \end{vmatrix}$$
Note that the blue ones have replaced zeros without changing the determinant. Now the lower right $7\times 7$ symmetric submatrix $M$ is a Cayley-Menger matrix which must have rank strictly less than $6$ and therefore a nullity of at least $2$. More verbosely, there exists a $k=2$-dimensional subspace of $\mathbb{R}^7$ upon which $M$ operates like a zero. This essentially removes $k(k+1)/2=3$ degrees of freedom from $M$. We will use that fact to eliminate the unknowns $D_{16},D_{25},D_{34}$. However, we won't try to find eigenspaces; instead we will employ the equivalent but more practical condition that the adjugate matrix of $M$ must be zero. That gives a lot of equations, though not all of those are independent.
If you had abundant time or computing power, you could try the following Sage script:
R.<W,D12,D13,D14,D15,D16,D23,D24,D25,D26,D34,D35,D36,D45,D46,D56> = QQ[]
KM = matrix(R, [
[0, 0, 0, 1, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 1, 0, 0, 1, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1],
[1, 0, 1, 0, D12, D13, D14, D15, D16],
[0, 1, 1, D12, 0, D23, D24, D25, D26],
[0, 0, 1, D13, D23, 0, D34, D35, D36],
[0, 0, 1, D14, D24, D34, 0, D45, D46],
[0, 1, 1, D15, D25, D35, D45, 0, D56],
[1, 0, 1, D16, D26, D36, D46, D56, 0]
])
pv = KM.det() - 2*W # Octahedron's volume formula; W = (12*V)^2
CM = KM[2:,2:] # Cayley-Menger matrix, 7*7, rank less than 6
AM = CM.adjoint() # all entries constrained to be zero
# Many of the AM[i,j]==0 are redundant, but it does not hurt to give as many
# low-degree equations as we can; this helps finding a good ideal basis.
constraints = [AM[h,k] for h in range(7) for k in range(h+1)]
I = R.ideal([pv] + constraints)
J = I.elimination_ideal([D16,D25,D34]) # massive effort here
# Exactly one equation left: len(J.gens()) == 1
wpoly = J.gen(0)
That would get you a polynomial wpoly that, when set equal to zero, states the
algebraic relation between $W$ and the (non-diagonal) edge length squares.
Then you would just need to plug in the edge lengths, solve for $W$,
discard non-real or negative solutions, and finally compute $V=(\sqrt{W})/12$
for the remaining $W$.
Several solutions are possible because giving distances cannot recover orientation information; conceptually you might flip vertices beyond their neighbors and thus find other valid configurations with different shapes.
Unfortunately, carrying all those free edge length parameters around was so much of a burden for my version of Sage (and Maxima, and Singular) that I had to abort the above computation. It took too long, or it ran out of memory.
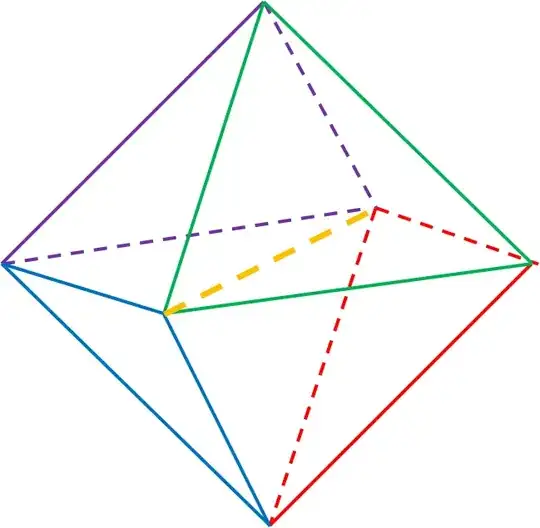
Let us simplify the case to what you have indicated in your drawing: Let $P_1$ be the leftmost vertex, $P_2$ foremost, $P_3$ downmost. Then set $$\begin{align} A &= D_{12} = D_{13} = D_{23} & B & = D_{14} = D_{15} = D_{45} \\ C &= D_{24} = D_{26} = D_{46} & D &= D_{35} = D_{36} = D_{56} \end{align}$$
That's only four free parameters. Alas, my old platform (or my patience) still cannot handle that.
Let's use a little trick. Replace $W$ with $F^3$. Then $F$ has the physical dimension of a squared length, as all the other parameters. Thus, the polynomial equation we seek between $A,B,C,D,F$ will be homogeneous. Equivalently, we can now fix $D = 1$, compute an inhomogeneous solution polynomial, and homogenize that again, thus recovering the correct power of $D$ in every monomial. This actually works:
R.<D16,D25,D34,F,W,A,B,C,D> = QQ[]
# W = F^3 = (12*Vol)^2
# Dij = squared distance between vertices i and j; diagonal iff i+j == 7
# A = D12 = D13 = D23
# B = D14 = D15 = D45
# C = D24 = D26 = D46
# D = D35 = D36 = D56
KM_full = matrix(R, [
[0, 0, 0, 1, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 1, 0, 0, 1, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1],
[1, 0, 1, 0, A, A, B, B, D16],
[0, 1, 1, A, 0, A, C, D25, C],
[0, 0, 1, A, A, 0, D34, D, D],
[0, 0, 1, B, C, D34, 0, B, C],
[0, 1, 1, B, D25, D, B, 0, D],
[1, 0, 1, D16, C, D, C, D, 0]
])
# To reduce computation effort, set D=1 and recover the powers of D by
# re-homogenizing the result polynomial.
KM = KM_full(D=1)
# All parameters represent lengths squared, therefore represent Vol^2 as F^3
# (do not use W here), so that re-homogenization makes sense.
pv = KM.det() - 2*F^3 # Octahedron's volume formula; F^3 = 144 Vol^2
CM = KM[2:,2:] # Cayley-Menger matrix, 7*7, rank less than 6
AM = CM.adjoint() # All entries constrained to be zero
constraints = [AM[h,k] for h in range(7) for k in range(h+1)]
# Many of the AM[i,j]==0 are redundant, but it does not hurt to give as many
# low-degree equations as we can; this helps finding a good ideal basis.
I = R.ideal([pv] + constraints)
J = I.elimination_ideal([D16,D25,D34]) # now done within minutes
# Exactly one equation left: len(J.gens()) == 1
# Reconstruct powers of D
fpoly = J.gen(0).homogenize(var=D)
# Note: fpoly.degree(F) == 24
# Exponents of F in fpoly are always divisible by 3, i.e.
# uniq(t[3] % 3 for t in fpoly.exponents()) == [0]
# Rewrite in terms of W, up to W^8
wcoeffs = [fpoly.coefficient({F:3*i}) for i in xrange(fpoly.degree(F)/3 + 1)]
wpoly = sum(c*W^i for i,c in enumerate(wcoeffs))
# Checking the result without homogenization tricks:
KM = KM_full
pv = KM.det() - 2*W # Octahedron's volume formula; W = 144 Vol^2
CM = KM[2:,2:] # Cayley-Menger matrix, 7*7, rank less than 6
AM = CM.adjoint() # all entries constrained to be zero
constraints = [AM[h,k] for h in range(7) for k in range(h+1)]
I = R.ideal([pv] + constraints)
wpoly in I # True
save(wpoly, "octa-wpoly.sobj") # save for later re-use
Example and sanity test: Regular octahedron with edge length $3\sqrt{2}$:
wpoly = load("octa-wpoly.sobj")
R = wpoly.parent()
D16,D25,D34,F,W,A,B,C,D = R.gens()
weq = wpoly(A=18,B=18,C=18,D=18).univariate_polynomial()
weq.roots(ring=RR, multiplicities=False) # [0., 186624.]
sqrt(max(weq.roots(ring=RR, multiplicities=False)))/12 # 36.
P.S.: I have chosen the constant factor in $W$ such that the coefficients of wpoly have small constant factors.
Resultant. Easy-peasy! – Blue Dec 24 '18 at 16:23