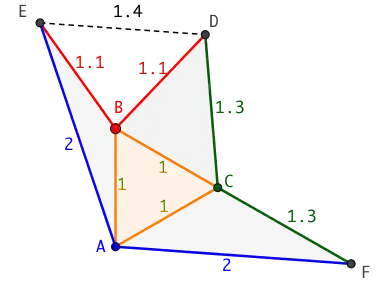
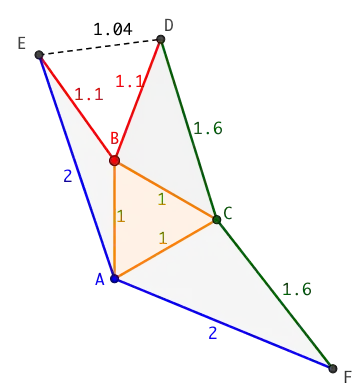
Let $A_1, A_2, A_3, A'_1, A'_2, A'_3$ be the vertices of a (not-necessarily convex) octahedron; here $X'$ is the vertex not on an edge with $X$. Suppose that the four non-adjacent triangular faces $A_1 A_2 A_3$, $A_1 A'_2 A'_3$,$A'_1 A_2 A'_3$,$A'_1 A'_2 A_3$ are equilateral with sides of lengths $x_0, x_1, x_2, x_3$.
I am interested in knowing the conditions on $x_0,x_1,x_2,x_3$ that must be satisfied for such a configuration to exist; and how unique the configuration is. This is a preliminary step to understanding this Question on Octahedra and the answer by @Blue.
Clearly it is necessary that $x_i>0$ for each $i$; and by using the triangle inequality on the other four faces, that $x_i+x_j>x_k$ for every 3-set $\{i,j,k\}\subset \{0,1,2,3\}$.
Question 1: are these conditions sufficient for existence? I think so, but have only a hand-waving argument and would like something better.
It seems to me that if such a configuration exists for some $x_0,x_1,x_2,x_3$ then in general if we fix $A_2, A_3, A'_1, A'_2, A'_3$ there are two points $A_1$ which satisfy the right conditions, giving a convex octahedron and a non-convex one. Again I can only wave my hands, and my intuition may be wrong. So,
Question 2: what can be proved about uniqueness?
Lastly, to get some feeling for which $(x_0,x_1, x_2,x_3)$ yield an octahedron, I would like to understand their geometry.
Question 3: Describe geometrically the (subset of) the solid bounded by
\begin{align*} x_0+x_1+x_2+x_3&=1;&\\ x_i&=0, &i=0,\dots,3; \\ x_i+x_j&=x_k &\textrm{ for every 3-set } \{i,j,k\}\subset \{0,1,2,3\} \end{align*}
which yield solutions.