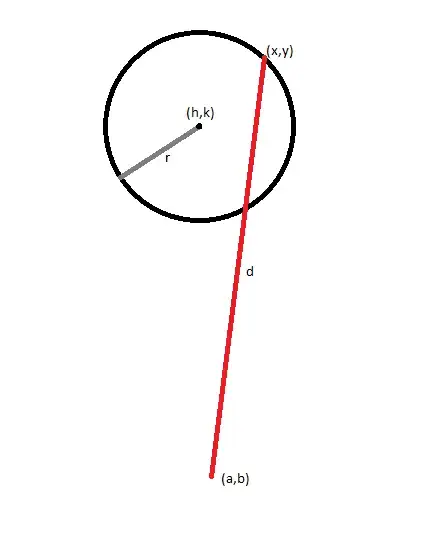
Given the length and one endpoint of the line segment, how can we find the other endpoint so that it is on the radius of a circle (known coordinates and radius)?
Assume that there is at least one solution.
All variables on the diagram are known except x and y.
If $d$ is suitable (you said assume there's a solution), the solutions will come from finding the intersection of the two circles $$(x-h)^2+(y-k)^2=r^2 \qquad\text{and}\qquad (x-a)^2+(y-b)^2=d^2.$$ This turns into solving one quadratic and one linear equation. You'll have a unique solution when $d=\sqrt{(h-a)^2+(k-b)^2}\pm r$, two solutions if $d$ is between those numbers, and no solutions otherwise.
