Collecting proofs for $\sum_{n=2}^{\infty} \, \frac{n-1}{2^n} = 1$

Question

Update: The summation I came across has the form shown in title, and that exact question appears to be new. I could ask for proofs that take on this summation directly (without reducing it to summations starting at $n = 0$ or $n =1$), and that would be the preferred answer and the only one I will accept. But might as well let this fly as is, collecting all proofs of the identified equivalent variants.

I just stumbled across the fact that

$\tag 1 \sum_{n=2}^{\infty} \, \frac{n-1}{2^n} = 1$ This is equivalent to $\tag 2 \sum_{n=1}^{\infty} \, \frac{n}{2^n} = 2$

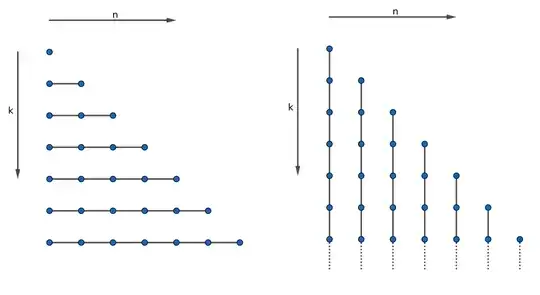
I discovered $\text{(1)}$ using a 'matrix/combinatorial' argument, but it would need work to turn it into a formal proof.

I googled and found this Quora link, explaining how to show $\text{(2)}$.

I didn't find the question on this site, prompting this 'collecting proofs post':

Please supply a proof demonstrating either $\text{(1)}$ or $\text{(2)}$. If you use any theory or technique, mention that at the start of your answer.

Answer 1

A probability theory flavored approach: The expression $\sum_{n\geq1} \frac{n}{2^n}$ is also the expected number of IID fair coin flips it takes to gets a heads. Assuming you know this number is finite (by some root/ratio test business), let $H$ be the expected time. Then from conditioning on seeing heads or tails on the first flip, respectively, $H$ satisfies the recursion $$H = \frac{1}{2}(1) + \frac{1}{2}(H+1),$$ so $H = 2$.

---

A brute-force approach: by induction or otherwise, $$\sum_{k=1}^n \frac{k}{2^k} = 2 - \frac{n+2}{2^n}.$$ Sending $n \to \infty$ recovers the desired result.

Answer 2

One approach is to note that for $S_k:=\sum_{n\geq k}\frac{1}{2^n}$ you have $S_0=2$ and $S_{k+1}=\frac{1}{2}S_k$. Now rearranging terms in the summation yields $$\sum_{n\geq1}\frac{n}{2^n} =\sum_{n\geq1}\sum_{k=1}^n\frac{1}{2^n} =\sum_{k\geq1}\sum_{n\geq k}\frac{1}{2^k},$$ corresponding to the following picture: The inner sums equal the $S_k$, so we can simplify this to $$\sum_{k\geq1}S_k =\sum_{k\geq1}\frac{1}{2^k}S_0 =S_0\sum_{k\geq1}\frac{1}{2^k}=S_0S_1=2.$$

Answer 3

We have that for $|x|<1$ by

$$f(x)=\sum_{k\ge1} x^n=\frac x{1-x} \implies f'(x)=\sum_{k\ge1} nx^{n-1}=\frac1{(1-x)^2}$$

therefore

$$\sum_{k\ge1} nx^{n}=x\cdot \sum_{k\ge1} nx^{n-1}=\frac x{(1-x)^2}$$

Answer 4

The standard technique is $\sum_{n\ge 1}r^n=\frac{1}{1-r}-1\implies\sum_{n\ge 1}nr^{n-1}=\frac{1}{(1-r)^2}$.

Answer 5

A solution by examining the differences between successive terms.

Let us define

$$S = \sum_{n=1}^{\infty} \, \frac{n}{2^n} = \sum_{n=1}^{\infty} u_n$$

Note (Edit): the definition $u_n = \frac{n}{2^n}$ will be used for $n=0$, i.e. for a term not involved in the series.

We have:

$$u_n - u_{n+1} = \frac{n-1}{2^{n+1}} = \frac{u_{n-1}}{4}$$

It follows immediately:

$$0 = S - S = \sum_{n=1}^{\infty} u_n - \sum_{n=1}^{\infty} u_{n+1} -u_1 = -u_1 + \frac{u_0}{4} + \frac{S}{4} $$

And therefore, noting that $u_0=0$ and $u_1 = \frac{1}{2}$ $$ S = \sum_{n=1}^{\infty} \, \frac{n}{2^n} = 2 $$

Note: the same procedure can be used to show that $$ \sum_{k=1}^n \frac{k}{2^k} = 2 - \frac{n+2}{2^n} $$

Answer 6

I stumbled on this by realizing that since

$$ \tag 1 \sum_{n=1}^{\infty} \, \frac{1}{2^n} = 1$$

it must be true that

$$ \tag 2 (\sum_{n=1}^{\infty} \, \frac{1}{2^n}) \times (\sum_{n=1}^{\infty} \, \frac{1}{2^n}) = 1$$

Using the rearrangement approach (and the identity $\sum_1^n \, 1 = n$) found in Servaes' answer,

$$ \tag 3 (\sum_{n=1}^{\infty} \, \frac{1}{2^n}) \times (\sum_{m=1}^{\infty} \, \frac{1}{2^m}) = \sum_{n+m =k}^{\infty} \, \frac{1}{2^k} = \sum_{k=2}^{\infty} \, \frac{k-1}{2^k} = 1$$

demonstrating the identity equation.