Prelude
This Post is a continuation of this Original Post. The original problem asked is:
How many solutions does the following equation have:
$$ a^x = \log_a(x) \,,\quad a \in (0,1) \wedge x \in\mathbb{R}^+_0 $$
And already has been answered (see Claude Leibovici's answer for details).
Observations
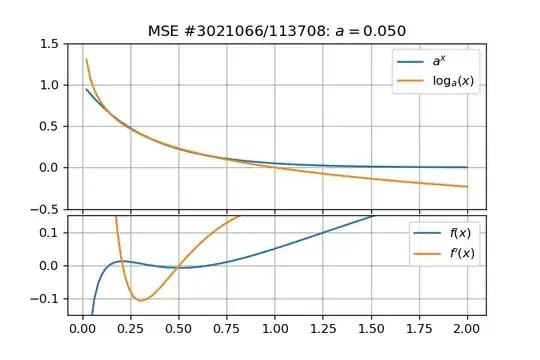
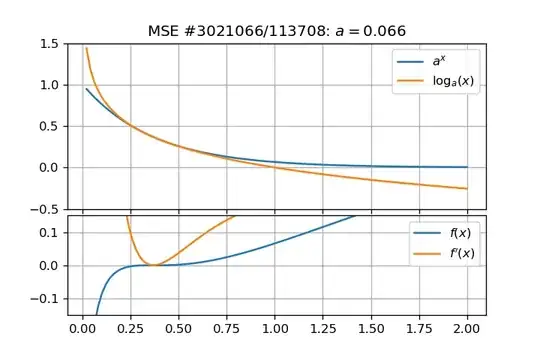
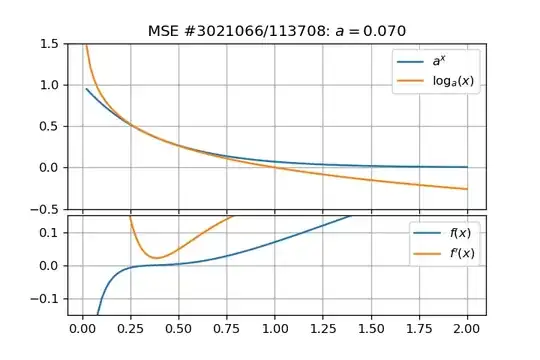
I found this problem interesting and I numerically investigated it a bit deeper. This led me to another question. Figures below show that such roots exist and are reals:
And roots can be computed numerically for several values of $a$:
My observations, so far, are:
- All roots must lie in $(0,1)$ because $\log_a(x) > 0 \, \forall x \in (0,1)$ and $\log_a(x) < 0$ elsewhere, and $a^x > 0 \,\forall x \in \mathbb{R}$;
- Solving this problem involves complex analysis (such as the use of Lambert W function) but the result will stay in the real domain;
- A "divergence" point occurs at $(e^{-e},e^{-1})$;
- Solving the original problem is equivalent to solve (base conversion and Lambert W properties):$$\ln(a) = \frac{W\left(x \ln(x)\right)}{x} = \frac{\ln(x)}{x} \Leftrightarrow a_k = \exp\left[\frac{W_k\left(x \ln(x)\right)}{x}\right]$$
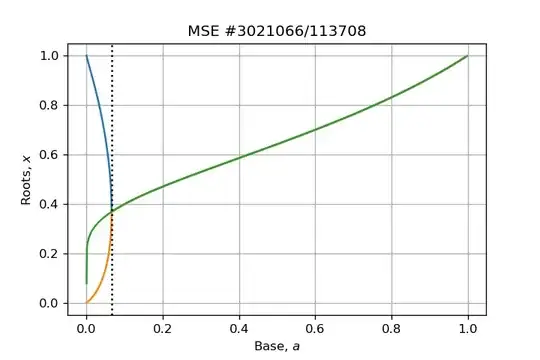
- Roots become triple when $a < e^{-e}$ (dashed black vertical line, as shown by Claude Leibovici in his answer)
Roots have asymptotic behavior, it can be checked in term of $a(x)$ for two branches:
- one root tends to unity as $a\rightarrow 1$: $\lim\limits_{x\rightarrow 1} a = 1$ (green curve rightmost);
- two roots tend to zero as $a\rightarrow 0^+$: $\lim\limits_{x\rightarrow 0^+} a = 0$ (green and orange curves leftmost).
Questions:
My main questions are:
How can I prove that one root tends to unity when base $a\rightarrow 0^+$ (blue curve leftmost)?By taking the limit of the proper branch.Is the point 4 correct?Investigating the solution using Wolfram Alpha it seems both Leibovici and my expressions are equivalent. But the first form suffer a huge float arithmetic error withnumpylibrary. Anyway they can be plotted using the latter form:
Side questions are:
- How is called the point where branches diverge?
- Do end of the branches also have a specific name?
Can we say that roots are multiple at the "divergence" point? If so, in what sense are they multiple?Claude Leibovici: Roots are multiple in the sense that three first degrees of Taylor expansion vanishes at $x=e^{-1}$ with $a=e^{-e}$.- Is the green branch a specific one because it behaves smoothly?
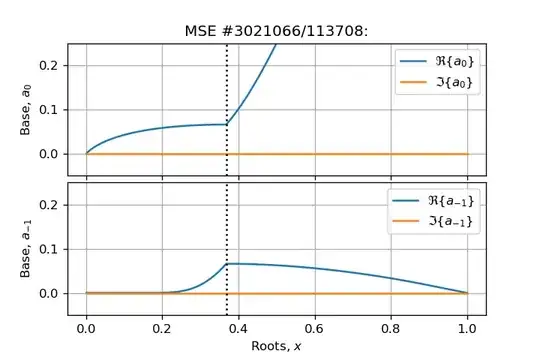
numpybut I succeed with another form (looks like a float error propagation I think it is due to the fractional power that grows quickly as $x \rightarrow 0$). Anyway Wolfram seems to show that both our versions agree. – jlandercy Dec 04 '18 at 09:17