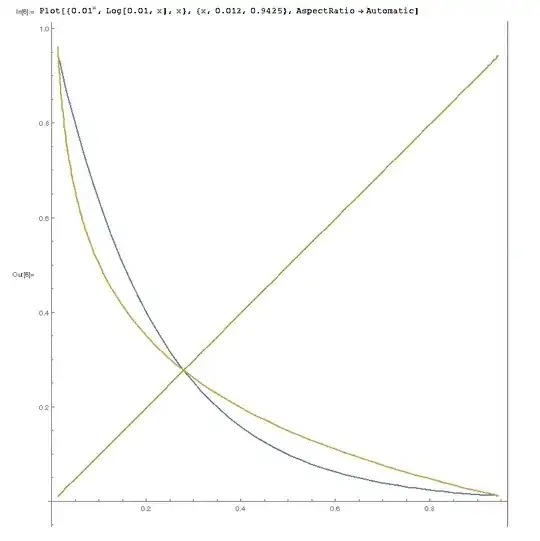
Too complex for a quiz.
Consider that you look for the zero's of function
$$f(x)=a^x-\frac{\log (x)}{\log (a)}$$ Its derivative is given by
$$f'(x)=a^x \log (a)-\frac{1}{x \log (a)}$$ this cancels at two points given by
$$x_1=\frac{W_0\left(\frac{1}{\log (a)}\right)}{\log (a)}\qquad \text{and}\qquad x_2=\frac{W_{-1}\left(\frac{1}{\log (a)}\right)}{\log (a)}$$ where appears Lambert function. In the real domain, we need $a \lt e^{-e}$. When this is the case, $f(x_1)>0$ and $f(x_2) < 0$ and in this range $\lim_{x\to 0} \, f(x)=\infty$. So, for $0 < a < e^{-e}$, there are three roots (the first one between $0$ and $x_1$; the second one between $x_1$ and $x_2$; the third one above $x_2$); for $a=e^{-e}$, there is a triple root and for $a>e^{-e}$, there is a single root.
Edit
Since this is an interesting numerical problem, I give you below the three roots for a faw values of $a$
$$\left(
\begin{array}{cccc}
a & \text{first root} & \text{second root} & \text{third root} \\
0.00500 & 0.005883 & 0.256675 & 0.969312 \\
0.01000 & 0.013093 & 0.277987 & 0.941488 \\
0.01500 & 0.021585 & 0.292615 & 0.913335 \\
0.02000 & 0.031462 & 0.304205 & 0.884194 \\
0.02500 & 0.042894 & 0.314008 & 0.853652 \\
0.03000 & 0.056133 & 0.322619 & 0.821327 \\
0.03500 & 0.071532 & 0.330371 & 0.786783 \\
0.04000 & 0.089601 & 0.337471 & 0.749451 \\
0.04500 & 0.111117 & 0.344056 & 0.708514 \\
0.05000 & 0.137359 & 0.350225 & 0.662661 \\
0.05500 & 0.170721 & 0.356048 & 0.609472 \\
0.06000 & 0.216898 & 0.361580 & 0.543230 \\
0.06500 & 0.303124 & 0.366862 & 0.436682 \\
0.06510 & 0.306379 & 0.366965 & 0.433018 \\
0.06520 & 0.309837 & 0.367069 & 0.429151 \\
0.06530 & 0.313538 & 0.367172 & 0.425041 \\
0.06540 & 0.317536 & 0.367275 & 0.420633 \\
0.06550 & 0.321911 & 0.367378 & 0.415848 \\
0.06560 & 0.326787 & 0.367481 & 0.410562 \\
0.06570 & 0.332376 & 0.367584 & 0.404564 \\
0.06580 & 0.339098 & 0.367686 & 0.397432 \\
0.06590 & 0.348099 & 0.367789 & 0.388021 \\
0.06591 & 0.349246 & 0.367799 & 0.386833 \\
0.06592 & 0.350471 & 0.367810 & 0.385567 \\
0.06593 & 0.351791 & 0.367820 & 0.384206 \\
0.06594 & 0.353233 & 0.367830 & 0.382723 \\
0.06595 & 0.354836 & 0.367840 & 0.381079 \\
0.06596 & 0.356672 & 0.367851 & 0.379202 \\
0.06597 & 0.358881 & 0.367861 & 0.376952 \\
0.06598 & 0.361865 & 0.367871 & 0.373927
\end{array}
\right)$$
For $a=e^{-e}$, the triple root is $0.367882$.
For the case of a single root
$$\left(
\begin{array}{cc}
a & \text{ root} \\
0.10 & 0.399013 \\
0.15 & 0.436709 \\
0.20 & 0.469622 \\
0.25 & 0.500000 \\
0.30 & 0.528956 \\
0.35 & 0.557154 \\
0.40 & 0.585043 \\
0.45 & 0.612961 \\
0.50 & 0.641186 \\
0.55 & 0.669965 \\
0.60 & 0.699535 \\
0.65 & 0.730133 \\
0.70 & 0.762013 \\
0.75 & 0.795457 \\
0.80 & 0.830785 \\
0.85 & 0.868378 \\
0.90 & 0.908699 \\
0.95 & 0.952326
\end{array}
\right)$$