I have some problem with awareness of school material. How can we say that $\cos\phi$ or $\sin\phi$ would be negative? The metric - a function that takes only positive values in $\mathbb{R}$. I know that in school about that sayng that $\phi$ -- obtuse angle. But for now it is looking little bit strange.
Asked
Active
Viewed 518 times
1 Answers
2
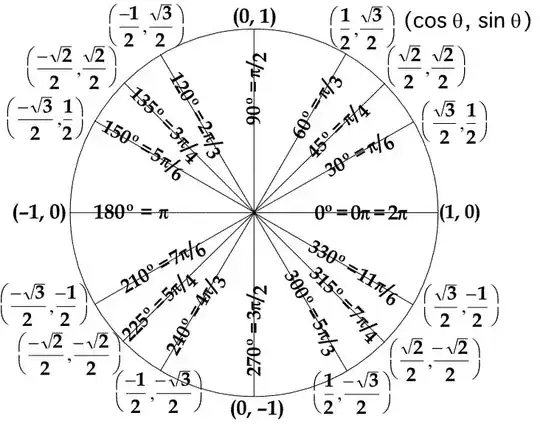
To understand that we need to recall that by definition $\cos \theta$ and $\sin \theta$ are precisely the coordinates of the point $P(x,y)$ on the unitary circle such that ray OP forms an angle $\theta$ with positive $x$ axis (usually assuming as positive the counterclockwise direction).
Since the equation for the unit circle is $x^2+y^2=1$, $\cos A$ and $\sin A$ can also assume negative values, for exampleat an angle $180°$ corresponds the point $(-1,0)$ and therefore
- $\cos (180°)=-1$
- $\sin (180°)=0$
user
- 154,566
-
Ye, I am thinking about that trig notation of $c\in\mathbb{C}$ can using the negative $\cos$ and $\sin$. But my intuition of metrics is broken – Just do it Dec 02 '18 at 09:00
-
@Arsenii Are you referring to $$\cos \theta = \frac{e^{i\theta}+e^{-i\theta} }2$$ – user Dec 02 '18 at 09:02
-
I dont know what is this :D I am about $z = a+bi = |z|(\frac{a}{|z|} + \frac{b}{|z|} i)$, where $a$ and $b$ can be negative real number – Just do it Dec 02 '18 at 09:04
-
@Arsenii That's exactly the trigonometric (polar) representation of complex numbers via trigonometric functions. According to the given definition $a/|z| = \cos \theta$ and $y/|z| = \sin \theta$. – user Dec 02 '18 at 09:06
-
1
-
-
real-analysistag tocomplex-numberswould also be appropriate). Perhaps also explain how your confusion about metrics is involved. As it is, the quesiton is a bit vague. – Blue Dec 02 '18 at 09:16