I must compute the following integral
$$\displaystyle\int_{0}^{+\infty}\frac{\log x}{1+x^3}dx$$
Can someone suggest me the right circuit in the complex plane over which to do the integration? I tried different paths, avoiding the origin, but unsuccessfully
Evaluating the integral $$ \int_\gamma\frac{\log(z)}{1+z^3}\,\mathrm{d}z\tag{1} $$ over the contour
$\hspace{4.5cm}$
and accounting for the pole at $e^{\pi i/3}$ with residue $\frac{\pi i}{3}\frac1{3e^{2\pi i/3}}$ gives $$ \begin{align} 2\pi i\frac{\pi i}{3}\frac1{3e^{2\pi i/3}} &=\color{#C00000}{\int_0^\infty\frac{\log(t)}{1+t^3}\,\mathrm{d}t} \color{#0000FF}{-\int_0^\infty\frac{\log(t)+2\pi i/3}{1+t^3}\,e^{2\pi i/3}\,\mathrm{d}t}\\ &=\left(1-e^{2\pi i/3}\right)\int_0^\infty\frac{\log(t)}{1+t^3}\,\mathrm{d}t -\frac{2\pi i}{3}e^{2\pi i/3}\int_0^\infty\frac{\mathrm{d}t}{1+t^3}\tag{2} \end{align} $$ Therefore, $$ \frac{2\pi^2}{9}e^{\pi i/3} =\left(1-e^{2\pi i/3}\right)\int_0^\infty\frac{\log(t)}{1+t^3}\,\mathrm{d}t +\frac{2\pi}{3}e^{\pi i/6}\int_0^\infty\frac{\mathrm{d}t}{1+t^3}\tag{3} $$ Dividing by $e^{\pi i/3}$ $$ \frac{2\pi^2}{9} =-i\sqrt3\int_0^\infty\frac{\log(t)}{1+t^3}\,\mathrm{d}t +\frac{\pi(\sqrt3-i)}{3}\int_0^\infty\frac{\mathrm{d}t}{1+t^3}\tag{4} $$ The real part of $(4)$ yields $$ \int_0^\infty\frac{\mathrm{d}t}{1+t^3}=\frac{2\pi\sqrt3}{9}\tag{5} $$ and the imaginary part of $(4)$ combined with $(5)$ gives $$ \int_0^\infty\frac{\log(t)}{1+t^3}\,\mathrm{d}t=-\frac{2\pi^2}{27}\tag{6} $$
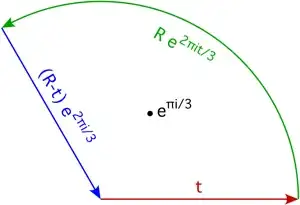
This one may also be solved using a keyhole contour as follows. Consider
$$\oint_C dz \frac{\log^2{z}}{1+z^3}$$
Note that we are using the square of the log here. Over the keyhole contour, note that we pass over the positive real axis twice: once for $\arg{z}=0$, then back again for $\arg{z}=2 \pi$. One can show that the integral over the circular contours (large and small) will vanish as the radius of the large contour goes to infinity, and the small one goes to zero.
In the meantime, we are left with the integrals over the real axis. Note that the log function is multivalued in the following sense:
$$\log{(x e^{i 2 \pi})} = \log{x} + i 2 \pi$$
so that the integral over $C$ boils down to
$$\begin{align}\oint_C dz \frac{\log^2{z}}{1+z^3} &= \int_0^{\infty} dx \frac{\log^2{x}}{1+x^3} - \int_0^{\infty} dx\frac{(\log{x}+ i 2 \pi)^2}{1+x^3}\\ &= -i 4 \pi \int_0^{\infty} dx \frac{\log{x}}{1+x^3} + 4 \pi^2 \int_0^{\infty} dx \frac{1}{1+x^3} \end{align}$$
Don't worry about that second integral on the RHS for now. As you can see, though, we have reproduced our original integral.
Now, by the Residue Theorem, the contour integral is equal to $i 2 \pi$ times the sum of the residues of the poles of the integrand within $C$. We have poles where $1+z^3=0$, but it is very important how we express them. The poles are at $e^{i \pi/3}$, $-1$, and $e^{i 5 \pi/3}$. Note that in the latter, we did not use $e^{-i \pi/3}$, although in most cases it wouldn't matter. Here, because we are dealing with a multivalued function, it does.
The residues at these simple poles are as follows:
$$\mathrm{Res}_{z=-1} = \frac{-\pi^2}{(1+e^{i \pi/3}) (1+e^{-i \pi/3})}$$ $$\mathrm{Res}_{z=e^{i \pi/3}} = \frac{-(\pi^2/9)}{(e^{i \pi/3}-e^{-i \pi/3}) (1+e^{i \pi/3})}$$ $$\mathrm{Res}_{z=e^{-i \pi/3}} = \frac{-(25\pi^2/9)}{(1+e^{-i \pi/3}) (e^{-i \pi/3}-e^{i \pi/3})}$$
I will spare you the arithmetic involved in combining and simplifying these. Our equation for the integrals becomes
$$-i 4 \pi \int_0^{\infty} dx \frac{\log{x}}{1+x^3} + 4 \pi^2 \int_0^{\infty} dx \frac{1}{1+x^3} = i 2 \pi \left ( \frac{4 \pi^2}{27} - i \frac{4 \pi^2}{3 \sqrt{3}} \right ) $$
Equating real and imaginary parts, we get
$$\int_0^{\infty} dx \frac{\log{x}}{1+x^3} = -\frac{2 \pi^2}{27}$$ $$\int_0^{\infty} dx \frac{1}{1+x^3} = \frac{2 \pi}{3 \sqrt{3}}$$
So we get a bonus integral for free.
Let $$I = \int_0^{\infty} \dfrac{\log(x)}{1+x^3} dx = \underbrace{\int_0^1 \dfrac{\log(x)}{1+x^3} dx}_J + \underbrace{\int_1^{\infty} \dfrac{\log(x)}{1+x^3} dx}_K$$ $$K = \int_1^{\infty} \dfrac{\log(x)}{1+x^3} dx = \int_1^0 \dfrac{\log(1/x)}{1+1/x^3} \left(-\dfrac{dx}{x^2}\right) = - \int_0^1 \dfrac{x \log(x)}{1+x^3} dx$$ Now recall that $$\int_0^1 x^m \log(x) dx = - \dfrac1{(m+1)^2}$$ Hence, $$J = \int_0^1 \dfrac{\log(x)}{1+x^3} dx = \int_0^1 \sum_{k=0}^{\infty}(-x^3)^k \log(x) dx = \sum_{k=0}^{\infty}(-1)^k \int_0^1 x^{3k} \log(x) dx = \sum_{k=0}^{\infty} \dfrac{(-1)^{k+1}}{(3k+1)^2}$$ $$K = -\int_0^1 \dfrac{x\log(x)}{1+x^3} dx = \sum_{k=0}^{\infty}(-1)^{k+1} \int_0^1 x^{3k+1} \log(x) dx = \sum_{k=0}^{\infty} \dfrac{(-1)^{k}}{(3k+2)^2}$$ Hence, $$J = -\sum_{k=0}^{\infty} \dfrac1{(6k+1)^2} + \sum_{k=0}^{\infty} \dfrac1{(6k+4)^2} = f_4 - f_1$$ $$K = \sum_{k=0}^{\infty} \dfrac1{(6k+2)^2} - \sum_{k=0}^{\infty} \dfrac1{(6k+5)^2} = f_2 - f_5$$ where $$f_l = \sum_{k=0}^{\infty} \dfrac1{(6k+l)^2}$$ Note that $f_6 = \dfrac{\pi^2}{216}$, $f_3 = \dfrac19 \cdot \dfrac{\pi^2}8 = \dfrac{\pi^2}{72}$. Let $\zeta$ be the $6^{th}$ root of unity i.e. $\zeta = e^{\pi i /3}$.
We have $$\text{Li}_2(\zeta) = \sum_{k=1}^{\infty} \dfrac{\zeta^k}{k^2} = \zeta f_1 + \zeta^2 f_2 - f_3 - \zeta f_4 - \zeta^2 f_5 + f_6 = - \dfrac{\pi^2}{108} - \zeta J + \zeta^2 K$$ $$\text{Li}_2(\zeta^5) = \sum_{k=1}^{\infty} \dfrac{\zeta^{5k}}{k^2} = \zeta^5 f_1 + \zeta^{10} f_2 + \zeta^{15} f_3 + \zeta^{20} f_4 + \zeta^{25} f_5 + f_6 = - \dfrac{\pi^2}{108} + \zeta^2 J - \zeta K$$ where $\text{Li}_s(x)$ is the polylogarithm function defined as $$\text{Li}_s(x) = \sum_{k=0}^{\infty} \dfrac{x^k}{k^s}$$ Polylgarithm function satisfies a nice identity namely $$\text{Li}_n(e^{2 \pi ix}) + (-1)^n \text{Li}_n(e^{-2 \pi ix}) = - \dfrac{(2\pi i)^n}{n!}B_n(x)$$ where $B_n(x)$ are Bernoulli polynomials. Take $n=2$ and $x = 1/6$ to get that $$\text{Li}_2(\zeta) + \text{Li}_2(\zeta^5) = - \dfrac{(2\pi i)^2}{2!}B_2(1/6) = - \dfrac{(2\pi i)^2}{2!} \dfrac1{36} = \dfrac{\pi^2}{18}$$ Hence, \begin{align} \zeta^2(J+K) - \zeta(J+K) - \dfrac{\pi^2}{54} & = \dfrac{\pi^2}{18}\\ \overbrace{(\zeta^2-\zeta)}^{-1}(J+K) & = \dfrac{\pi^2}{18} + \dfrac{\pi^2}{54}\\ -(J+K) & = \dfrac{2\pi^2}{27} \end{align} Hence, $$I = J+K = -\dfrac{2 \pi^2}{27}$$
This one may be done by parameterization. Introduce $f(t)$ where $$ f(t) = \int_0^\infty \frac{x^t}{1+x^3} dx$$ where $0\le t \le 1,$ so that we are looking for $f'(0).$ Let $\rho$ be the singularity in the first quadrant, so that $$\operatorname{Res}\left(\frac{x^t}{1+x^3}; x=\rho\right) = \frac{\rho^t}{3\rho^2}.$$ Now use a slice contour to evaluate $f(t)$, starting at the origin and going to $R$ on the real axis, moving along an arc to $R e^{2\pi i/3}$ and then straight back to the origin, so that $\rho$ is the only singularity inside the contour and it is easy to see that the contribution of the arc disappears in the limit (because our choice of the domain of $t$).
The intgral along the rotated line segment is $$ e^{2\pi i/3} \int_R^0 \frac{(e^{2\pi i/3} x)^t}{1 + e^{2\pi i}x^3} dx = - (e^{2\pi i/3})^{t+1} \int_0^R \frac{x^t}{1+x^3} dx$$
It follows by the Cauchy residue theorem that $$ f(t) = 2\pi i \frac{\rho^{t-2}/3}{1- (e^{2\pi i/3})^{t+1}}.$$ Recall that $\rho = e^{\pi i/3}$, so that $$ f(t) = 2\pi i \frac{\rho^{t-2}/3}{1- (\rho^2)^{t+1}}.$$ Now differentiate with respect to $t$ to get $$ f'(t) = {\frac {2/3\,i\pi \, \left( {\rho}^{t-2}\ln \left( \rho \right) -{\rho}^{t} \ln \left( \rho \right) \left( {\rho}^{2} \right) ^{t}+{\rho}^{t} \left( { \rho}^{2} \right) ^{t}\ln \left( {\rho}^{2} \right) \right) }{ \left( -1+ \left( {\rho}^{2} \right) ^{t}{\rho}^{2} \right) ^{2}}} $$ so that $f'(0)$ is $$2/3\,i\pi \, \left( {\frac {\ln \left( \rho \right) }{{\rho}^{2}}}-\ln \left( \rho \right) +\ln \left( {\rho}^{2} \right) \right) \left( -1+{\rho} ^{2} \right) ^{-2}\\ = 2/3\,i\pi \, \left( {\ln \left( \rho \right) }-\rho^2 \ln \left( \rho \right) + \rho^2\ln \left( {\rho}^{2} \right) \right) \left( -\rho+{\rho} ^{3} \right) ^{-2} \\ = 2/3\,i\pi \, \left( {\ln \left( \rho \right) }-\rho^2 \ln \left( \rho \right) + \rho^2\ln \left( {\rho}^{2} \right) \right) \left( -\rho-1 \right) ^{-2} \\ = 2/3\,i\pi \, \ln\rho\left(1-\rho^2 + 2\rho^2 \right) \left( -\rho-1 \right) ^{-2} \\ = 2/3\,i\pi \, \ln\rho\left(1+\rho^2\right) \left(\rho+1 \right) ^{-2}.$$ We are justified in writing $\ln \rho^2 = 2\ln\rho$ because $\rho^2$ stays in the upper half plane and does not cross the branch cut of the logarithm.
To conclude, re-introduce the value for $\rho$ to get $$f'(0) = -\frac{2\pi^2}{27}.$$
