0

A friend has given me this task and asked for help. I immediately tried picking various $f$ and $g$ such that $g$ and $g\circ f$ are both surjective but $f$ is not. However, i always found myself restricting $\mathbb{R}$ to some subsets $A \subset \mathbb{R}$ in order to make it work. I can't figure out how to prove it for

$$ \mathbb{R} \xrightarrow{f} \mathbb{R} \xrightarrow{g} \mathbb{R}$$

Is it even possible? I also tried using sectionwise defined functions (different functions for $x \ge 0$ and $x < 0$). However, no success.

Any advise? I'm starting to assume that it's not possible for $\mathbb{R}$ without any restrictions.

Thanks for any help!

Zest
  • 2,418

3 Answers3

1

For all real numbers $x$ we have $\log(e^{x})=x$. Take $f(x)=e^{x}, g(x)=\log\, x$ if $x>0$ and $g(x)=0$ for $x\leq 0$.

Kavi Rama Murthy
  • 311,013
  • that was exactly my very first approach. However, the domain of $\log(x)$ is $\mathbb{R}^+$. I assume you've chosen $f(x) = e^x$ and $g(x) = \ln(x)$, didnt you? – Zest Nov 17 '18 at 23:36
  • @Zest See my revised answer. – Kavi Rama Murthy Nov 17 '18 at 23:40
  • Regarding your revides answer: That was basically my second approach which i initially thought would solve it. But that results in $(f \circ g)(x)$ not being surjective, doesn't it? – Zest Nov 17 '18 at 23:42
  • @Zest Are you saying that the identity function $x \to x$ is not surjective? – Kavi Rama Murthy Nov 17 '18 at 23:45
  • for every negative $x \in \mathbb{R}$ you have $f(g(x)) = f(0) = e^0 = 1$.

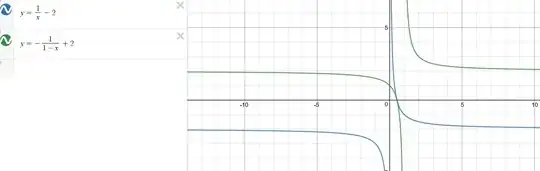
    for every positive $x \in \mathbb{R}$ you get $f(g(x)) = x$.

    so we have $(f \circ g)(x) = 1$ for all $x \le 0$ and $(f \circ g)(x) = x$ for all $x > 0$, i dont think this is surjective tbh. There is no $x$ such that $(f \circ g)(x) = -3$ for example.

     – Zest Nov 17 '18 at 23:53
  • @Zest Why are you computing $f\circ g$? Don't you have $g\circ f$ in the question? Note that $g(f(-3))=g(e^{-3})=\log, e^{-3}=-3$. – Kavi Rama Murthy Nov 17 '18 at 23:57
  • Sorry, my bad. It was simply a typo. We are looking at $g \circ f$ indeed. – Zest Nov 18 '18 at 00:00
1

Take, for instance,$$f(x)=\begin{cases}x&\text{ if }x\leqslant-1\\x+3&\text{ otherwise}\end{cases}\text{ and }g(x)=x^3-3x.$$It is clear that $f$ is not surjective. However,$$g\bigl(f(\mathbb{R})\bigr)=g\bigl((-\infty,-1]\cup(2,+\infty)\bigr)=\mathbb R.$$

José Carlos Santos
  • 427,504
  • this is exactly what i needed! thank you very much :-) i couldnt get it done myself. highly appreciating your help. – Zest Nov 17 '18 at 23:56
0

Consider $g:(0,1) \rightarrow \mathbb{R}$ enter image description here

$g(x)= \begin{array}{cc} \{ & \begin{array}{cc} \frac{1}{x} - 2 & x < \frac{1}{2} \\ \ \frac{-1}{1-x} + 2 & x >= \frac{1}{2} \\ \end{array} \} \end{array} $ enter image description here

and define $f: \mathbb{R} \rightarrow (0,1)$

$f(x)=\frac{1}{1+e^x}$ Is there a bijective map from $(0,1)$ to $\mathbb{R}$?

$g o f$ is surjective but $f$ is not.

user614287
  • 1,147