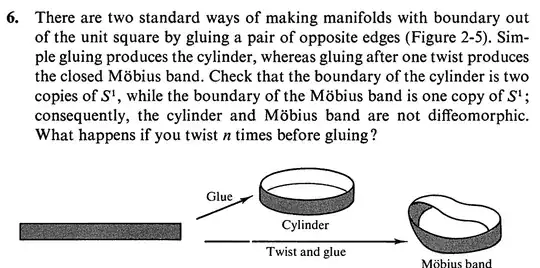
The question is given below:
I have made a Mobius band with a paper and twisted it 3-times but I could not describe what I see it may be a 3 knot shape, could anyone give me a hint for solving that question please?
EDIT:
The answer to my previous question is here:
Topologically distinguishing Mobius Strips based on the number of half-twists
But still I do not know how to prove that the boundary of the cylinder is 2 copies of $S^1$ and that of the Mobius band is 1 copy of $S^1$, could anyone help me in doing so?