Why is this way of deriving surface area of sphere wrong when a similar method can be used to derive volume?

Question

Suppose a sphere with radius R is centered at the origin, whose cross section is as follows (R is the constant radius while r is variable):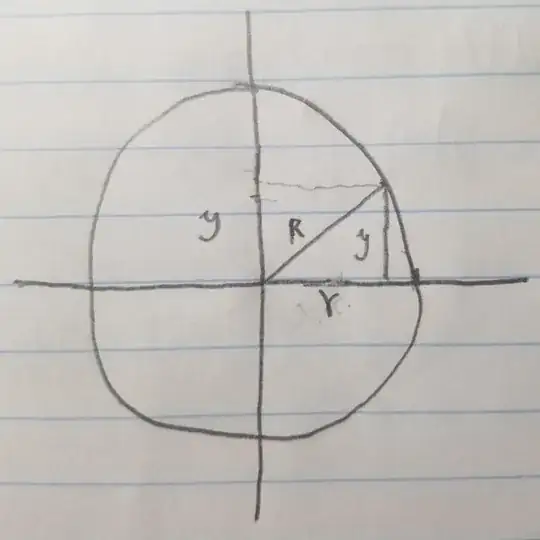 then its volume can be easily calculated:

$V=\int_{-R}^{R}\pi r^2 dy = \int_{-R}^{R}\pi (R^2-y^2) dy = \cfrac{4 \pi R^3} {3}$

This can be intuitively understood as summing up thin cylinders with base radius $r$ and height $dy$. However, if I try to do find the surface area by doing something similar: sum up rings with radius $r$ and thickness $dy$, I end up with

$A=\int_{-R}^{R} 2 \pi r dy=\int_{-R}^{R} 2 \pi \sqrt{R^2-y^2} dy = \pi^2 R^2$

which is completely wrong. Why is that the same approach works for deriving the volume formula while results in a wrong answer for surface area? Can this approach be modified to make it work for surface area? Thanks!

TL;DR: the little rings you’re adding up don’t approximate the surface area well enough. It’s the same sort of error that’s made in the “proof” that $\pi=4$. — amd, Nov 02 '18 at 01:19
Try thinking about arclength first. Can you get the length of a slanted (but non-vertical) line segment by adding up only the $\Delta y$'s? — Ted Shifrin, Nov 02 '18 at 02:08
See this answer https://math.stackexchange.com/a/1692595/72031 — Paramanand Singh, Nov 02 '18 at 02:51

score 3 · Answer 1 · answered Nov 02 '18 at 01:16

3

For your surface area the thickness $dy$ or $dx$ does not count the slope of the surface.

You need to use $ds=\sqrt{1+(\frac {dy}{dx})^2}dx$

answered Nov 02 '18 at 01:16

Mohammad Riazi-Kermani

68,728

score 0 · Answer 2 · answered Nov 02 '18 at 02:02

0

This is famous high school integral's fail example. Although you sum up $\int 2\pi r dy$, cone is expressed like same $\int2\pi r dy$, why so.

answered Nov 02 '18 at 02:02

Takahiro Waki

2,310

Why is this way of deriving surface area of sphere wrong when a similar method can be used to derive volume?

2 Answers2

Linked

Related