2

Polynomials over $\mathbb{Q}$ can exhibit "geometrical symmetries" in different ways, graph-wise (as functions $P:\mathbb{R} \rightarrow \mathbb{R}$) and root-wise:

  • $P(x) = P (-x)$
    (axial symmetry along $y$-axis)

  • $P(x) = -P (x)$
    (central symmetry)

  • $P(x) = \prod_{k=-n}^n (x + k)$: all roots are real and have the same consecutive distance
    (translational symmetry)

  • $P(x) = \sum_{k=0}^{2n} x^k$: all roots are complex, have the same norm and the same consecutive distance
    (rotational symmetry)

  • For each polynomial $P(x)$ the complex roots come in conjugate pairs.
    (axial symmetry along $x$-axis)

I wonder which other "geometrical symmetries" of polynomials, their graphs and their roots are there - and how these symmetries do possibly relate to the permutational symmetries as reflected in the Galois group of a polynomial.

Hans-Peter Stricker
  • 18,159
  • Note: To get full translational symmetry, $P(x)=P(x+1)$, you need to work over a field of finite characteristic instead over $\Bbb{Q}$. Otherwises the translated zeros bleed over the edge. – Jyrki Lahtonen Oct 18 '18 at 10:46
  • Would you accept polynomial in several variables? I believe that is necessary to get symmetries of order, say, three. – Jyrki Lahtonen Oct 18 '18 at 10:46
  • Yes, I should have said (and originally did) "some sort of translational/rotational symmetry". – Hans-Peter Stricker Oct 18 '18 at 10:47

1 Answers1

2

You can get rotational symmetry of arbitrary order for the set of real zeros of bivariate polynomials.

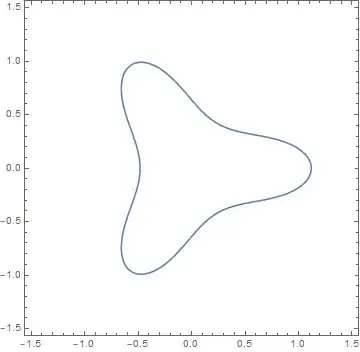
One way of generating such polynomials is to use the arithmetic of complex numbers. For hopefully obvious reason the cubic $$ R_3(x,y):=\operatorname{Re}\left((x+iy)^3\right)=x^3-3xy^2 $$ has the property that if $(x',y')$ is the point we get by rotating $(x,y)$ 120 degrees about the origin, then $R_3(x',y')=R_3(x,y)$.

Therefore it is obvious that the set of solutions of the polynomial equation $$(x^3-3xy^2)+\frac16=(x^2+y^2)^2$$ exhibits this 3-fold rotational symmetry.

enter image description here

Similarly using $R_5(x,y)=\operatorname{Re}\left((x+iy)^5\right)=x^5-10x^3y^2+5xy^4$ we get 5-fold rotational symmetry in the zero locus of the polynomial $$(x^5-10x^3y^2+5xy^4)+1-(x^2+y^2)^3.$$

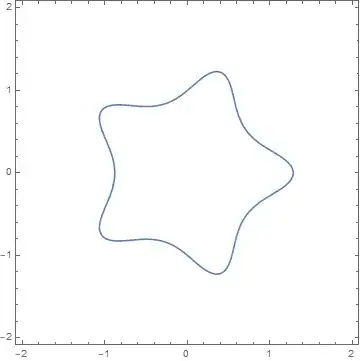
enter image description here

I included a non-zero constant term and a high enough power of $(x^2+y^2)$ to guarantee that the set of solutions is a compact subset of $\Bbb{R}^2$, and that there is no singularity at the origin.

A few more remarks:

  • The above curves actually have full dihedral symmetry, if you want to kill reflections as symmetries you can do tricks like those I used here.
  • You can similarly find polynomials in $n$ variables such that their zero sets have any given finite group of $n\times n$ matrices as a symmetry.
  • It is rare that the Galois group of a univariate polynomial has a nice geometrical interpretation. The dihedral groups do make an appearance as Galois groups of, say, $x^3-2$ or $x^4+2$, when the set of complex zeros exhibits a similar geometric dihedral symmetry (actually matching with the action of the Galois group on the set of roots).
  • A reasonably often occurring symmetry among the roots of an irreducible polynomial is the case of the minimal polynomial $f_p(x)$ (over $\Bbb{Q}$) of $\alpha=2\cos(2\pi/p)$, $p>2$ a prime. Then we have the "symmetry" that if $r$ is a zero of $f(x)$, so is $r^2-2$. This comes from the fact that $2\cos2x=4\cos^2x-2=(2\cos x)^2-2$. If $m$ is not divisible by $p$ the formula for $\cos mx$ as a polynomial of $\cos x$ can similarly be translated into another symmetry among the roots.
Jyrki Lahtonen
  • 133,153
  • Not sure whether you actually ok'd bivariate polynomials. If you think of this as cheating then I will delete. No problem, no hard feelings. – Jyrki Lahtonen Oct 18 '18 at 12:18