7

I like to visualize everything I study but yet I have found pretty nothing to visualize in abstract algebra.I have studied group theory upto subgroups Cyclic groups and Cosets and Lagrange's theorem.Is there any way of visualizing these things?Please suggest some good reference book/text also which discusses these things and also the motivation/idea behind different theorems and concepts.

  • 4
    Group theory can be visualized as groups of symmetries. – Michael Burr Jun 06 '19 at 13:14
  • See also https://math.stackexchange.com/q/1327016/589 and https://math.stackexchange.com/questions/607436/what-do-polynomials-look-like-in-the-complex-plane and The Fundamental Theorem of Algebra: A Visual Approach by Velleman. – lhf Jun 06 '19 at 13:38
  • 3
    Cayley graphs provide a way to visualize groups. There is a textbook called Visual Group Theory that gives visual interpretations for many group theoretic properties. – Viktor Vaughn Jun 06 '19 at 13:41
  • I seem to recall a book by Fraleigh (First Course on Abstract Algebra) which had some visuals to go with quotient groups/cosets. Also simply the vertices of a regular $n-gon$ are a starting point for visualising subgroups of the finite cyclic groups. – Mark Bennet Jun 06 '19 at 18:07
  • Is the pdf available on internet? –  Jun 06 '19 at 18:15
  • 1
    There is a reason it called "abstract algebra" but there is ofcourse there are some ways to visualize it (if not all). But I am not sure if you have that enough background yet or not? – Anubhav Mukherjee Jun 06 '19 at 21:55
  • You can just visualize it in terms of sets and maps. I think that's the best that we can do in most generality. – Someone Jun 06 '19 at 23:23
  • I have had the same problem, as a student. I started to make sense of group theory much later, when I started to get interested in continuous groups, in the context of differential equations. Seeing an application of the abstract concepts, I started to also automatically build visual images of them. (I have never properly studied Galois theory, but I guess that it will provide the same amount of application of finite groups than Lie theory and differential equations provide for continuous groups). In summary, my advice is to just soldier on. Visualization will arise later. – Giuseppe Negro Jun 07 '19 at 08:41
  • Thank you very much. –  Jun 07 '19 at 13:45

2 Answers2

6

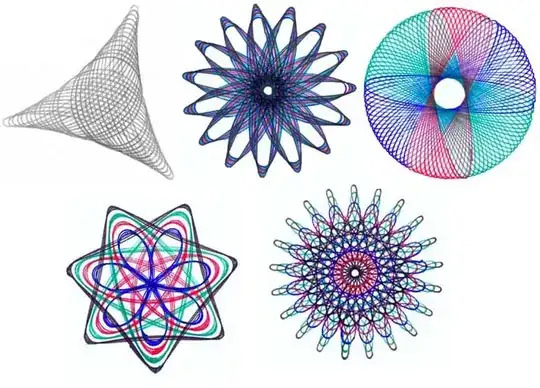
One nice visual approach to basic results on cyclic groups is using periodical curves such as Roulettes (Spirograph curves), Star Polygons, etc. Some of these have concrete implementations in toys like Spirograph - which can be employed to motivate these more abstract algebraic ideas at very elementary levels.

enter image description here

Community
  • 1
Bill Dubuque
  • 272,048
  • Do the colors in the images have any meaning or are they there to make them pretty? – B.Swan Jun 06 '19 at 16:35
  • So how do you use these pictures to visualize the concepts? – Rushabh Mehta Jun 06 '19 at 18:00
  • Tell me something more on the above pictures as Don Thousand said? –  Jun 06 '19 at 18:15
  • @KishalaySarkar Sure, I'll elbaorate in a bit. – Bill Dubuque Jun 06 '19 at 18:45
  • 1
    If the OP wants plane curves with cyclic symmetry groups then there are simpler versions like this with a 3-fold rotational symmetry. Complex power mappings lead to simple equations. Here is a 5-fold symmetry. I didn't bother to kill the dihedral symmetry of the latter curve. Sorry about that. Can't offer curves related to toys or pieces of art either :-( – Jyrki Lahtonen Jun 06 '19 at 20:03
  • @JyrkiLahtonen No, the point is to use the star polygons (and related objects) as visualizations of subgroups of cyclic groups (and their cosets). which also helps with visualizing related number-theoretic concepts (Bezout's identity, Gauss's algorithm for modular inversion, etc). – Bill Dubuque Jun 06 '19 at 20:21
4

To add a bit of history here - the famous German mathematician Felix Klein in 1872 launched the so-called Erlangen Program, proposing a method of characterizing geometries based on group theory and projective geometry. This was a novel and visionary idea a the time of his writings. It preceded later developments that showed how the symbiosis of (Complex) Analysis, Geometry and Algebra led to new insights and theories.

Nicky Hekster
  • 49,281