11

I have a triangle $ABC$ and I want to construct a square of the same area as that of the triangle using ruler and compass.

Consider the following image.

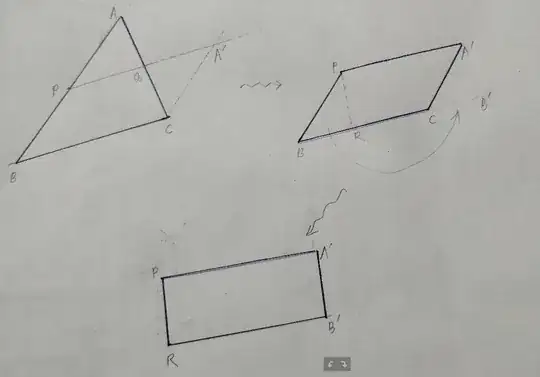
I first locate the mid-points of $AB$ and $BC$ and draw a line parallel to $AB$ passing through $C$. Say this line intersects $PQ$ at $A'$. Then chopping off $APQ$ and putting it in place of $A'QC$ leads to the parallelogram $PA'CB$.

Dropping perpendiculars from $P$ and $A'$ to $BC$ gives points $R$ and $B'$. Chopping off the triangle $PBR$ from the paralellogram and sliding it to coincide with the imaginary triangle $A'CB'$ leads to the rectangle $PRB'A'$.

Now I want to convert this rectangle into a square. I could do something like Job Bouwman's answer here but that construction does not have the spirit of "chopping off and rearranging the pieces to obtain a square".

Can somebody see as to how to go about hacking away at the rectangle and make the pieces fall into the shape of a square?

Thank you.

caffeinemachine
  • 18,510
  • Start with the rectangle that you have. I like this construction of quadrature of the rectangle based on Euclid's theorem, but it does not give a cut-and-rearrange the pieces method http://serge.mehl.free.fr/exos/quadra_rect.html – user376343 Oct 07 '18 at 16:22

1 Answers1

12

Given a rectangle with side lengths $a,b$ we want to construct a square of the same area. Without loss of generality assume $a>b$.

The first step is to obtain the square's side length $m=\sqrt{ab}$. This is a classical construction; erect a semicircle on a segment of length $a+b$ and draw the perpendicular from a point $a$ from one end. The length of that perpendicular within the semicircle is $m$.

The actual cuts to the rectangle that transform it into a square are based off a 2016 paper on illustrating the Bolyai–Gerwien theorem. From one vertex draw a cut to the long opposite side, creating a right triangle with legs $m$ and $b$. On the long side incident to said vertex, erect a perpendicular cut at the point $a-m$ from the vertex that stops at the first cut (this second cut has length $m-b$). This creates three pieces, which rearrange into a square, as shown above.

If $a>4b$, the above construction will not work. In this case, repeatedly bisect the rectangle parallel to its short side and stack the halves on top of each other until $a\le4b$.

Parcly Taxel
  • 103,344