5

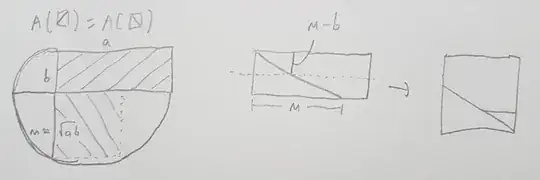
There are several propositions and constructions in Euclid's Elements that relate to the squaring of a rectangle, e.g.

  • Proposition II.5: If a straight line is cut into equal and unequal segments, then the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section equals the square on the half.
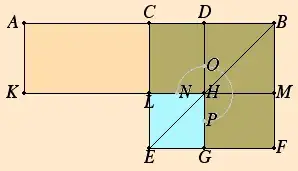
    enter image description here

  • Proposition II.14: To construct a square equal to a given rectilinear figure.
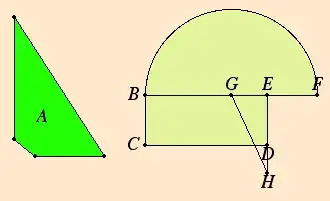
    enter image description here

  • Proposition VI.13: To find a mean proportional to two given straight lines.
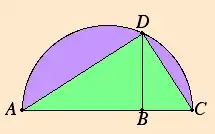
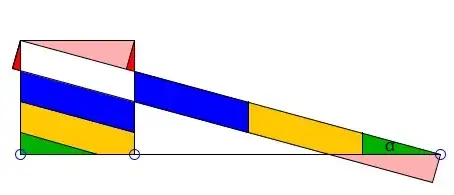
    enter image description here

But none of these resemble the "proof without words" (which isn't found in the Elements) that any rectangle can be dissected and rearranged to obtain an equal square:

enter image description here

Performing this dissection essentially means to construct the angle $\alpha$ - everything else follows.

My question is:

How do I specifically construct the angle $\alpha$ when given an arbitrary rectangle?

Hans-Peter Stricker
  • 18,159

2 Answers2

5

You do not actually have to construct $\alpha$. This is the diagram I drew for a very similar question, only with "rectangle" replaced by "triangle". Then again, I went through a rectangle in order to get to a square.

I recap what I said. In what follows, $a>b$ are the rectangle's sides and $m=\sqrt{ab}$ is their geometric mean.

From one vertex draw a cut to the long opposite side, creating a right triangle with legs $m$ and $b$. On the long side incident to said vertex, erect a perpendicular cut at the point $a-m$ from the vertex, that stops at the first cut (this second cut has length $m-b$). This creates three pieces, which rearrange into a square.

If $a>4b$, bisect the rectangle parallel to its short side and stack the halves on top of each other until $a\le4b$.

Community
  • 1
Parcly Taxel
  • 103,344
1

First construct (CAR) the square size.

Reference : Compass-and-straightedge construction of the square root of a given line?

You rotate your rectangle horizontally (put rectangle largest edge below AB). Intersect circle center A radius h (height of rectangle, smallest edge) with AB to get C (like on picture to get C-A-B). So AC = h. Draw semicircle centered midpoint of CB through C and B. Intersect with orthogonal line to AB through A to get D. Because of similarities : AC/AD = AD/AB implying AD^2 = h AB. So AD is square size.

Then construct alpha.

Draw another picture with a long segment (AE..) with square size ADFE on it. Intersect circle center D length AB with the long segment.

Dominique Laurain
  • 61